题目内容
(本题满分14分)二次函数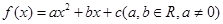 满足条件:
满足条件:
①当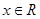 时,
时,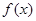 的图象关于直线
的图象关于直线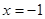 对称;
对称;
② 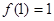 ;
;
③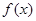 在
在 上的最小值为
上的最小值为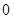 ;
;
(1)求函数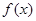 的解析式;
的解析式;
(2)求最大的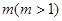 ,使得存在
,使得存在 ,只要
,只要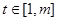 ,就有
,就有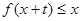 .
.
【答案】
解:(1)∵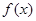 的对称轴为
的对称轴为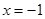 ,
,
∴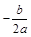 = –1即
= –1即 ………………1分
………………1分
又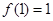 ,即
,即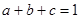 …………………………2分
…………………………2分
由条件③知: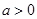 ,且
,且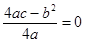 ,即
,即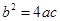 ……………………3分
……………………3分
由上可求得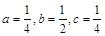 ……………………4分
……………………4分
∴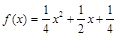 …………………………5分.
…………………………5分.
(2)由(1)知: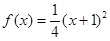 ,图象开口向上.
,图象开口向上.
而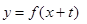 的图象是由
的图象是由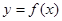 平移
平移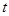 个单位得到,要
个单位得到,要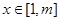 时,
时, 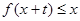 即
即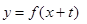 的图象在
的图象在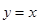 的图象的下方,且
的图象的下方,且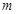 最大.……7分
最大.……7分
∴1,m应该是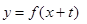 与
与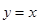 的交点横坐标,……………………8分
的交点横坐标,……………………8分
即1,m是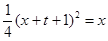 的两根,…………………………9分
的两根,…………………………9分
由1是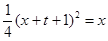 的一个根,得
的一个根,得 ,解得
,解得 ,或
,或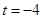 …11分
…11分
把 代入原方程得
代入原方程得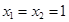 (这与
(这与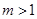 矛盾)………………12分
矛盾)………………12分
把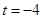 代入原方程得
代入原方程得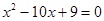 ,解得
,解得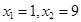 ∴
∴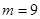 ……13分
……13分
综上知: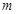 的最大值为9.……………………14分
的最大值为9.……………………14分
【解析】略

练习册系列答案
相关题目
 +
+ 的图象通过原点,对称轴为
的图象通过原点,对称轴为 ,
, .
. 是
是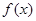 的导函数,且
的导函数,且
 );
); 满足
满足 ,且
,且 ,求数列
,求数列 ,
, ,是否存在自然数
,是否存在自然数 ,使得当
,使得当 时
时
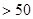 恒成立?若存在,求出最小的
恒成立?若存在,求出最小的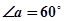 ,
,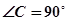 ,
,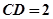 。
。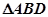 沿BD折起(如图二),使二面角A-BD-C的余弦值等于
沿BD折起(如图二),使二面角A-BD-C的余弦值等于 。对于图二,
。对于图二,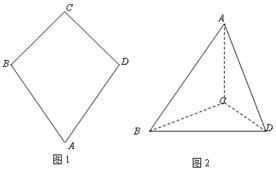
 的长,并证明:
的长,并证明: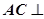 平面
平面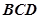 ;
; 所成角的正弦值。
所成角的正弦值。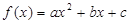 .
. ,方程
,方程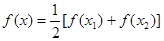 有2个不等实根,
有2个不等实根,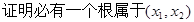 ;
;