Question

如图,在棱长为1的正方体ABCD—A₁B₁C₁D₁中,P是侧棱CC₁上的一点,CP=m.

(1)试确定m,使得直线AP与平面BDD₁B₁所成角的正切值为;

(2)在线段A₁C₁上是否存在一个定点Q,使得对任意的m,D₁Q在平面APD₁上的射影垂直于AP?证明你的结论.

Answer 1

解析:(1)连结AC,设AC∩BD=O,AP与面BDD₁B₁交于点G,连结OG,因为PC∥面BDD₁B₁,面BDD₁B₁∩面APC=OG,故OG∥PC,所以OG=PC=.

又AO⊥DB,AO⊥BB₁,所以AO⊥面BDD₁B₁.

故∠AGO即为AP与面BDD₁B₁所成的角.

在Rt△AOG中,tan∠AGO=,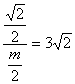

即m=,

故当m=时,直线AP与平面BDD₁B₁所成角的正切值为.

(2)依题意,要在A₁C₁上找一点Q,使得D₁Q⊥AP.

可推测A₁C₁的中点O₁即为所求的Q点.

因为D₁O₁⊥A₁C₁,D₁O₁⊥AA₁,所以D₁O₁⊥面ACC₁A₁.

又AP面ACC₁A₁,

故D₁O₁⊥AP.

从而D₁O₁在平面AD₁P上的射影与AP垂直.