[题目]函数f(x)=x2cosx在的图象大致是( )A.B.C.D. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】函数f（x）=x2cosx在的图象大致是（）
A.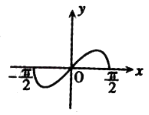
B.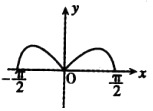
C.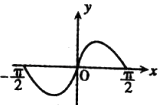
D.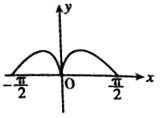

【答案】B
【解析】解：函数f（x）=x2cosx在，满足f（﹣x）=f（x），所以函数是偶函数，排除选项A，C；

当x∈（0，）时，f′（x）=2xcosx﹣x2sinx，令2xcosx﹣x2sinx=0，可得xtanx=2，方程的解x ，即函数的极大值点x ，排除D，

故选：B．

【考点精析】认真审题，首先需要了解函数的图象(函数的图像是由直角坐标系中的一系列点组成；图像上每一点坐标（x，y）代表了函数的一对对应值，他的横坐标x表示自变量的某个值，纵坐标y表示与它对应的函数值)，还要掌握函数的极值与导数(求函数的极值的方法是:（1）如果在附近的左侧,右侧,那么是极大值（2）如果在附近的左侧,右侧,那么是极小值)的相关知识才是答题的关键．

练习册系列答案

相关题目

【题目】设数列满足：① ；②所有项；③ ．
设集合，将集合中的元素的最大值记为．换句话说，是
数列中满足不等式的所有项的项数的最大值．我们称数列为数列的
伴随数列．例如，数列1,3,5的伴随数列为1,1,2,2,3．
（1）若数列的伴随数列为1,1,1,2,2,2,3，请写出数列；
（2）设，求数列的伴随数列的前100之和；
（3）若数列的前项和（其中常数），试求数列的伴随数列前项和．

【题目】已知函数f（x）=lnx﹣x2与g（x）=（x﹣2）2﹣ ﹣m的图象上存在关于（1，0）对称的点，则实数m的取值范围是（）
A.（﹣∞，1﹣ln2）
B.（﹣∞，1﹣ln2]
C.（1﹣ln2，+∞）
D.[1﹣ln2，+∞）

【题目】经市场调查，某商品每吨的价格为x（1＜x＜14）万元时，该商品的月供给量为y1吨，y1=ax+ a2﹣a（a＞0）：月需求量为y2吨，y2=﹣ x2﹣ x+1，当该商品的需求量大于供给量时，销售量等于供给量：当该商品的需求量不大于供给量时，销售量等于需求量，该商品的月销售额等于月销售量与价格的乘积．
（1）已知a= ，若某月该商品的价格为x=7，求商品在该月的销售额（精确到1元）；
（2）记需求量与供给量相等时的价格为均衡价格，若该商品的均衡价格不低于每吨6万元，求实数a的取值范围．

【题目】以下四个命题： ①已知随机变量X～N（0，σ2），若P（|X|＜2）=a，则P（X＞2）的值为；
②设a、b∈R，则“log2a＞log2b”是“2a﹣b＞1”的充分不必要条件；
③函数f（x）= ﹣（）x的零点个数为1；
④命题p：n∈N，3n≥n2+1，则￢p为n∈N，3n≤n2+1．
其中真命题的序号为．

【题目】若函数f（x）=x3﹣3ax+3a在区间（0，2）内有极小值，则a的取值范围是（　　）
A.a＞0
B.a＞2
C.0＜a＜2
D.0＜a＜4

【题目】设函数f（x）=x3+bx2+cx（x∈R），已知g（x）=f（x）﹣f′（x）是奇函数．
（Ⅰ）求b，c的值．
（Ⅱ）求g（x）的单调区间与极值．

【题目】执行如图的程序框图（N∈N*），那么输出的p是（）
A.
B.
C.
D.

【题目】某沿海四个城市A、B、C、D的位置如图所示，其中∠ABC=60°，∠BCD=135°，AB=80nmile，BC=40+30 nmile，CD=250 nmile，D位于A的北偏东75°方向．现在有一艘轮船从A出发以50nmile/h的速度向D直线航行，60min后，轮船由于天气原因收到指令改向城市C直线航行，收到指令时城市C对于轮船的方位角是南偏西θ度，则sinθ= ．

试题分类