题目内容
 的值域为________,
的值域为________, 的值域为________.
的值域为________.
[-4,-2] [-5,-1]
分析:(1)是形如y=asinx+bcosx的函数模型求值域,可以化为一个三角函数的名下处理.
(2)是形如y=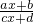 的函数模型求值域,可以想办法去掉分子的变量x,即利用反函数思想解决问题.
的函数模型求值域,可以想办法去掉分子的变量x,即利用反函数思想解决问题.
解答:(1) -4=2|sin(x-
-4=2|sin(x- )|-4,
)|-4,
∴0≤|sin(x- )|≤1,∴-4≤2|sin(x-
)|≤1,∴-4≤2|sin(x- )|-4≤-2
)|-4≤-2
故答案为:[-4,-2].
(2) y= =4-
=4- ,
,
∵-1≤cosx≤1,∴1≤cosx+2≤3,3≤ ≤9,
≤9,
∴-5≤4- ≤1,
≤1,
故答案为:[-5,-1].
点评:求函数值域的常见题型与方法:
(1)形如y=asinx+bcosx的函数模型,宜采用化简到同一三角函数名下处理.
(2)形如y=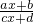 的函数模型,宜采用反函数法处理.
的函数模型,宜采用反函数法处理.
(3)形如y=(ax+b)+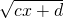 的函数模型,宜采用换元法处理.
的函数模型,宜采用换元法处理.
(4)复合函数模型,单调性遵循同增异减,值域需要知道构成复合的每一个函数的性质.
分析:(1)是形如y=asinx+bcosx的函数模型求值域,可以化为一个三角函数的名下处理.
(2)是形如y=
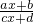 的函数模型求值域,可以想办法去掉分子的变量x,即利用反函数思想解决问题.
的函数模型求值域,可以想办法去掉分子的变量x,即利用反函数思想解决问题.解答:(1)
 -4=2|sin(x-
-4=2|sin(x- )|-4,
)|-4,∴0≤|sin(x-
 )|≤1,∴-4≤2|sin(x-
)|≤1,∴-4≤2|sin(x- )|-4≤-2
)|-4≤-2故答案为:[-4,-2].
(2) y=
 =4-
=4- ,
,∵-1≤cosx≤1,∴1≤cosx+2≤3,3≤
 ≤9,
≤9,∴-5≤4-
 ≤1,
≤1,故答案为:[-5,-1].
点评:求函数值域的常见题型与方法:
(1)形如y=asinx+bcosx的函数模型,宜采用化简到同一三角函数名下处理.
(2)形如y=
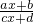 的函数模型,宜采用反函数法处理.
的函数模型,宜采用反函数法处理.(3)形如y=(ax+b)+
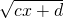 的函数模型,宜采用换元法处理.
的函数模型,宜采用换元法处理.(4)复合函数模型,单调性遵循同增异减,值域需要知道构成复合的每一个函数的性质.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目