题目内容
求函数y＝
(a＞0且a≠1)的定义域．
答案：
解析：
提示：
解析：
|
解：由1－loga(x＋a)≥0，得loga(x＋a)≤1． 当a＞1时，0＜x＋a≤a， ∴－a＜x≤0． 当0＜a＜1时，x＋a≥a，∴x≥0． 综上，当a＞1时，函数的定义域为(－a，0]． 当0＜a＜1时，函数的定义域为[0，＋∞)． 思路分析：先由被开方数是非负数建立不等式，由于不等式中含有字母参数，再根据对数的性质对字母参数进行分类讨论． |
提示：
|
对于对数函数问题，底数中含字母参数的都必须进行分类讨论． |
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
(a＞0)的图象关于y＝x对称．
，Sn)均在函数y＝f(x)上，求a的值，并求数列{
}的所有项的和(即前n项和的极限)．
＋6x的图象关于y轴对称．
(A＞0，
＞0，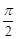
＜
＜
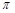)，x∈[－3，0]的图象，且图象的最高点为B(－1，
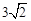)；赛道的中间部分为
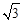千米的水平跑到CD；赛道的后一部分为以O圆心的一段圆弧
．
，求当“矩形草坪”的面积最大时
(A＞0，
＞0，
＜
＜
)，x∈[－3，0]的图象，且图象的最高点为B(－1，
)；赛道的中间部分为
千米的水平跑到CD；赛道的后一部分为以O圆心的一段圆弧
．
，求当“矩形草坪”的面积最大时