题目内容
设P为椭圆
＝1上的一点，F1，F2分别是该椭圆的左、右焦点，若|PF1|∶|PF2|＝2∶1，则△PF1F2的面积为( )．
＝1上的一点，F1，F2分别是该椭圆的左、右焦点，若|PF1|∶|PF2|＝2∶1，则△PF1F2的面积为( )．| A．2 | B．3 | C．4 | D．5 |
C
设P(x，y)，则由已知易知F1(－
，0)，F2(，0)．∵|PF1|∶|PF2|＝2∶1，且|PF1|＋|PF2|＝6，∴|PF1|＝4，|PF2|＝2，即
＝4，
＝2，两式联立可解得
得P
，∴△PF1F2的面积为
|F2F1|·|y|＝×2×
＝4.
，0)，F2(，0)．∵|PF1|∶|PF2|＝2∶1，且|PF1|＋|PF2|＝6，∴|PF1|＝4，|PF2|＝2，即＝4，＝2，两式联立可解得得P，∴△PF1F2的面积为|F2F1|·|y|＝×2×＝4.
练习册系列答案
星级口算天天练系列答案
相关题目
M为CD的中点.
，使
，且P点到A、B 的距离和为定值，求点P的轨迹E的方程；
的直线与轨迹E交于P、Q两点，求
面积的最大值．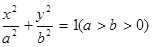
的离心率为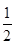
，左、右焦点分别为
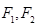，点G在椭圆C上，且
，
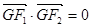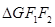的面积为3.
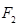的直线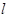
与椭圆交于不同的两点M，N（不同于点A，B），探索直线AM，BN的交点能否在一条垂直于
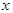轴的定直线上，若能，求出这条定直线的方程；若不能，请说明理由．
＋y2＝1，椭圆C2以C1的长轴为短轴，且与C1有相同的离心率．
＝2
，求直线AB的方程．
轴上，一个顶点为
，其右焦点到直线
的距离为
，则椭圆的方程为 ．
的左右焦点为
，若存在动点
，满足
，且
的面积等于
，则椭圆离心率的取值范围是 .
上一点，F1、F2为椭圆的左、右焦点，B为椭圆右顶点，若
平分线与
的平分线交于点
，则
.
的准线过椭圆
的左焦点且与椭圆交于A、B两点，O为坐标原点，
的面积为
，则椭圆的离心率为( )
B. 
C.
D.
的左顶点A且斜率为
的直线交椭圆
于另一点
，且点
轴上的射影恰为右焦点
,若
，则椭圆的离心率
的值是 .