题目内容
已知 ,
,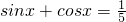 .
.
(1)求sinx-cosx的值;
(2)求 的值.
的值.
解:(1)∵ ,∴sinx<0,cosx>0,则sinx-cosx<0,
,∴sinx<0,cosx>0,则sinx-cosx<0,
又sinx+cosx= ,平方后得到 1+sin2x=
,平方后得到 1+sin2x= ,
,
∴sin2x=- ∴(sinx-cosx )2=1-sin2x=
∴(sinx-cosx )2=1-sin2x= ,
,
又∵sinx-cosx<0,
∴sinx-cosx=- .
.
(2)由(1)可得sinx=- ,cosx=
,cosx= ,tanx=-
,tanx=- ,
,
代入分子分母中,原分式可化为:
= =
=
分析:(1)由 可知x是第四象限角,从而sinx<0,cosx>0,由此可知sinx-cosx<0.再利用平方关系式求解.(sinx-cosx)2=(sinx+cosx)2-4sinxcosx.
可知x是第四象限角,从而sinx<0,cosx>0,由此可知sinx-cosx<0.再利用平方关系式求解.(sinx-cosx)2=(sinx+cosx)2-4sinxcosx.
(2)由(1)求出tanx,sinx,cosx代入分式即可得到答案.
点评:本题利用公式(sinx-cosx)2=(sinx+cosx)2-4sinxcosx.求解时需要开方,一定要注意正负号的取法,注意角x的范围.
 ,∴sinx<0,cosx>0,则sinx-cosx<0,
,∴sinx<0,cosx>0,则sinx-cosx<0,又sinx+cosx=
 ,平方后得到 1+sin2x=
,平方后得到 1+sin2x= ,
,∴sin2x=-
 ∴(sinx-cosx )2=1-sin2x=
∴(sinx-cosx )2=1-sin2x= ,
,又∵sinx-cosx<0,
∴sinx-cosx=-
 .
.(2)由(1)可得sinx=-
 ,cosx=
,cosx= ,tanx=-
,tanx=- ,
,代入分子分母中,原分式可化为:

=
 =
=
分析:(1)由
 可知x是第四象限角,从而sinx<0,cosx>0,由此可知sinx-cosx<0.再利用平方关系式求解.(sinx-cosx)2=(sinx+cosx)2-4sinxcosx.
可知x是第四象限角,从而sinx<0,cosx>0,由此可知sinx-cosx<0.再利用平方关系式求解.(sinx-cosx)2=(sinx+cosx)2-4sinxcosx.(2)由(1)求出tanx,sinx,cosx代入分式即可得到答案.
点评:本题利用公式(sinx-cosx)2=(sinx+cosx)2-4sinxcosx.求解时需要开方,一定要注意正负号的取法,注意角x的范围.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 如图,已知曲线
如图,已知曲线
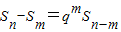 恒成立.
恒成立.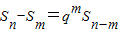 恒成立.
恒成立.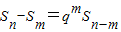 恒成立.
恒成立.