题目内容
如图，已知△ABC是正三角形，EA、CD都垂直于平面ABC，且EA=AB=2a，DC=a，F是BE的中点，
求证：（1）FD∥平面ABC；
（2）AF⊥平面EDB。
求证：（1）FD∥平面ABC；
（2）AF⊥平面EDB。
| 证明：（1）取AB的中点M，连FM，MC， ∵F、M分别是BE、BA的中点， ∴FM∥EA，FM=  EA， ∵EA、CD都垂直于平面ABC， ∴CD∥EA， ∴CD∥FM， 又DC=a， ∴FM=DC， ∴四边形FMCD是平行四边形， ∴FD∥MC， ∴FD∥平面ABC。 （2）因M是AB的中点，△ABC是正三角形， 所以CM⊥AB， 又CM⊥AE， 所以CM⊥面EAB，CM⊥AF，FD⊥AF， 因F是BE的中点，EA=AB， 所以AF⊥EB。 |
 |
练习册系列答案
相关题目
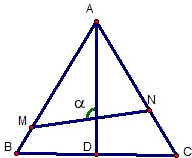如图，已知△ABC是边长为1的正三角形，M、N分别是边AB、AC上的点，线段MN经过△ABC的中心G，设?MGA=a（
20、如图，已知△ABC是正三角形，EA、CD都垂直于平面ABC，且EA=AB=2a，DC=a，F是BE的中点．
如图，已知△ABC是正三角形，EA、CD都垂直于平面ABC，且EA=AB=2a，DC=a，F是BE的中点，求证：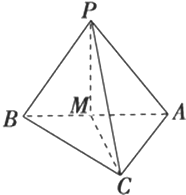
如图：已知△ABC是直角三角形，∠ACB=90°，M为AB的中点，PM⊥△ABC所在的平面，那么PA、PB、PC的大小关系是（ ）