题目内容
13.已知函数f(x)=sin(ωx-$\frac{π}{6}$)+cos(ωx-$\frac{π}{3}$)-2sin2$\frac{ωx}{2}$(ω>0)的周期为π.(I)求ω的值;
(Ⅱ)若x∈[0,$\frac{π}{2}$],求f(x)的最大值与最小值.
分析 (I)由条件利用三角恒等变换化简函数的解析式,再利用正弦函数的周期性得出结论.
(Ⅱ)由x∈[0,$\frac{π}{2}$],利用正弦函数的定义域和值域求得f(x)的值域.
解答 解:(I)∵函数f(x)=sin(ωx-$\frac{π}{6}$)+cos(ωx-$\frac{π}{3}$)-2sin2$\frac{ωx}{2}$
=sinωxcos$\frac{π}{6}$-cosωxsin$\frac{π}{6}$+cosωxcos$\frac{π}{3}$+sinωxsin$\frac{π}{3}$-2•$\frac{1-cosωx}{2}$
=$\sqrt{3}$sinωx+cosωx-1=2sin(ωx+$\frac{π}{6}$)-1(ω>0)的周期为$\frac{2π}{ω}$=π,∴ω=2.
(Ⅱ)若x∈[0,$\frac{π}{2}$],则2x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{7π}{6}$],∴sin(ωx+$\frac{π}{6}$)∈[-$\frac{1}{2}$,1],
∴f(x)=2sin(ωx+$\frac{π}{6}$)-1的值域为[-2,1].
点评 本题主要考查三角恒等变换,正弦函数的周期性,正弦函数的定义域和值域,属于中档题.

练习册系列答案
相关题目
4.在△ABC中,若$A=\frac{π}{6},a=2,b=2\sqrt{3}$,则B=( )
| A. | $\frac{π}{6}$或$\frac{5π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{3}$或$\frac{2π}{3}$ | D. | $\frac{2π}{3}$ |
2.下列语句是命题的是( )
| A. | 这房子大吗? | B. | 这是一棵大树呀! | ||
| C. | 我们班的男生不帅吗? | D. | 3.14是无理数 |
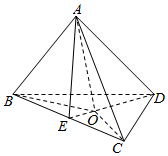 在平面几何里,有勾股定理:“设△ABC的两边AB、AC互相垂直,则AB2+AC2=BC2”.拓展到空间(如图),类比平面几何的勾股定理,研究三棱锥的侧面面积与底面面积间的关系,可以得出的结论是设三棱锥A-BCD的三侧面ABC,ACD,ADB两两垂直,则S△BCD2 =S△ABC2+S△ACD2+S△ADB2.
在平面几何里,有勾股定理:“设△ABC的两边AB、AC互相垂直,则AB2+AC2=BC2”.拓展到空间(如图),类比平面几何的勾股定理,研究三棱锥的侧面面积与底面面积间的关系,可以得出的结论是设三棱锥A-BCD的三侧面ABC,ACD,ADB两两垂直,则S△BCD2 =S△ABC2+S△ACD2+S△ADB2.