Question

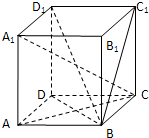如图，正方体ABCD-A₁B₁C₁D₁中，棱长为a
（1）求直线BC₁与AC所成的角；
（2）求直线D₁B与平面ABCD所成角的正切值；
（3）求证：平面BDD₁⊥平面ACA₁．

Answer 1

分析：（1）连接AD₁，D₁C，证明∠D₁AC为直线BC₁与AC所成的角，即可求得结论；
（2）利用DD₁⊥平面ABCD，可得∠D₁DB为直线D₁B与平面ABCD所成的角，利用正切函数可得结论；
（3）利用线面垂直的判定定理证明AC⊥平面BD₁D，再利用面面垂直的判定定理证明平面ACA₁⊥平面BD₁D．

解答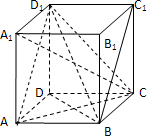：（1）解：连接AD₁，D₁C，则
∵ABCD-A₁B₁C₁D₁是正方体，∴四边形ABC₁D₁是平行四边形
∴A₁D₁∥DC₁，
∴∠D₁AC为直线BC₁与AC所成的角，
∵△AD₁C是等边三角形，
∴直线BC₁与AC所成的角为60°；
（2）解：∵DD₁⊥平面ABCD，∴∠D₁DB为直线D₁B与平面ABCD所成的角，
在Rt△D₁DB中，tan∠D₁DB=

1

2

=

2

2

∴直线D₁B与平面ABCD所成角的正切值为

2

2

；
（3）证明：∵DD₁⊥平面ABCD，AC?平面ABCD
∴DD₁⊥AC
∵BD⊥AC，BD∩DD₁=D
∴AC⊥平面BD₁D
∵AC?平面ACA₁，
∴平面ACA₁⊥平面BD₁D------（14分）

点评：本题考查空间角，考查面面垂直，考查学生分析解决问题的能力，解题的关键是正确作出空间角．