题目内容
点P(x,y)是椭圆 (a>b>0)上的任意一点,F1,F2是椭圆的两个焦点,且∠F1PF2≤90°,则该椭圆的离心率e的取值范围是
(a>b>0)上的任意一点,F1,F2是椭圆的两个焦点,且∠F1PF2≤90°,则该椭圆的离心率e的取值范围是
- A.

- B.

- C.(0,1)
- D.
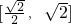
A
分析:由题设条件可知,当点P位于(0,b)或(0,-b)处时,∠F1PF2最大,此时 cos∠F1PF2= =
= ≥0,得到a和c之间的关系,由此能够推导出该椭圆的离心率的取值范围.
≥0,得到a和c之间的关系,由此能够推导出该椭圆的离心率的取值范围.
解答:由题意可知,当点P位于(0,b)或(0,-b)处时,∠F1PF2最大,
此时 cos∠F1PF2= =
= ≥0,∴a≥
≥0,∴a≥ c,
c,
∴e= ≤
≤ ,
,
又∵0<e<1,
∴0<e≤ .
.
故选A.
点评:本题考查椭圆的性质及其应用,难度不大,正确解题的关键是知道当点P位于(0,b)或(0,-b)处时,∠F1PF2最大.同时要注意椭圆离心率的取值范围是(0,1).
分析:由题设条件可知,当点P位于(0,b)或(0,-b)处时,∠F1PF2最大,此时 cos∠F1PF2=
 =
= ≥0,得到a和c之间的关系,由此能够推导出该椭圆的离心率的取值范围.
≥0,得到a和c之间的关系,由此能够推导出该椭圆的离心率的取值范围.解答:由题意可知,当点P位于(0,b)或(0,-b)处时,∠F1PF2最大,
此时 cos∠F1PF2=
 =
= ≥0,∴a≥
≥0,∴a≥ c,
c,∴e=
 ≤
≤ ,
,又∵0<e<1,
∴0<e≤
 .
.故选A.
点评:本题考查椭圆的性质及其应用,难度不大,正确解题的关键是知道当点P位于(0,b)或(0,-b)处时,∠F1PF2最大.同时要注意椭圆离心率的取值范围是(0,1).

练习册系列答案
相关题目