题目内容
过椭圆C：
外一点A（m，0）作一直线l交椭圆于P、Q两点，又Q关于x轴对称点为Q1，连结PQ1交x轴于点B，
（1）若
，求证：
；
（2）求证：点B为一定点(
，0)。
证明：（1）连结AQ1，因为Q与Q1关于x轴对称，而A在x轴上，
则在
中，AB平分
，
由内角平分线定理可知：
，
而
，
∵
同向，故λ＞0且
，则
，
又P、B、Q1在同一直线且
与
同向，
于是有：
。
（2）设过A（m，0）的直线l与椭圆C：
交于
，
Q1与Q关于x轴对称，则
，
由
及
相减得
，
∴
，
PQ直线方程：
，
而PQ过A（m，0），则有：
，
而PQ1过B
，同理可求得：
。
下面利用分析法证明：
，
即证：
， ……①
只需证：
，
只需证：
，
即证：
， ……②
而
在椭圆上，则
， ……③
同理
， ……④
由③×④可知②成立，从而①式得证，因此
成立。
∴
，∴点B为一定点（
，0）。
则在
中，AB平分，由内角平分线定理可知：
，而
，∵
同向，故λ＞0且，则，又P、B、Q1在同一直线且
与同向，于是有：
。（2）设过A（m，0）的直线l与椭圆C：
交于，Q1与Q关于x轴对称，则
，由
及相减得，∴
，PQ直线方程：
，而PQ过A（m，0），则有：
，而PQ1过B
，同理可求得：。下面利用分析法证明：
，即证：
， ……① 只需证：
，只需证：
，即证：
， ……② 而
在椭圆上，则， ……③ 同理
， ……④ 由③×④可知②成立，从而①式得证，因此
成立。∴
，∴点B为一定点（，0）。
练习册系列答案
相关题目
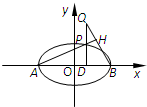如图，已知椭圆
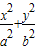=1（a＞b＞0）的离心率为
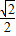，过原点O斜率为1的直线l与椭圆C相交于M，N两点，椭圆右焦点F到直线l的距离为
．
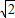=1（a＞b＞0）的离心率为
，过原点O斜率为1的直线l与椭圆C相交于M，N两点，椭圆右焦点F到直线l的距离为
．