题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,短轴长为
,短轴长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
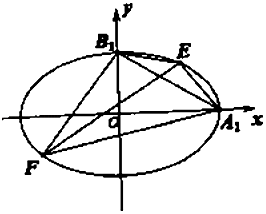
(2)设![]() ,
, ![]() 是椭圆
是椭圆![]() 上关于
上关于![]() 轴对称的任意两个不同的点,连接
轴对称的任意两个不同的点,连接![]() 交椭圆
交椭圆![]() 于另一点
于另一点![]() ,证明直线
,证明直线![]() 与
与![]() 轴相交于定点
轴相交于定点![]() ;
;
(3)在(2)的条件下,过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() ,
, ![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() .(2) 见解析.(3)
.(2) 见解析.(3) ![]() .
.
【解析】试题分析:⑴利用椭圆的定义和性质求出![]() ,
, ![]() ,即可求出椭圆的方程;⑵由题意知直线
,即可求出椭圆的方程;⑵由题意知直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]() ,由
,由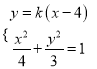 得
得![]() ,再由根与系数的关系证明直线
,再由根与系数的关系证明直线![]() 与
与![]() 轴相交于定点
轴相交于定点![]() ;⑶分
;⑶分![]() 的斜率存在与不存在两种情况讨论,与椭圆方程联立得出点
的斜率存在与不存在两种情况讨论,与椭圆方程联立得出点![]() 的坐标之间的关系,再表示出
的坐标之间的关系,再表示出![]() ,进而可求出其取值范围;
,进而可求出其取值范围;
解析:(1)由题意知![]() ,
,
又∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
解![]() ,得
,得![]() ,故椭圆
,故椭圆![]() 的方程为
的方程为![]() .
.
(2)由题意知直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]() ,
,
由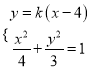 得
得![]() .①
.①
设点![]() ,
, ![]() ,则
,则![]() ,
,
直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得![]() ,将
,将![]() ,
, ![]() 代入,
代入,
整理,得![]() .②
.②
由①得![]() ,
, ![]() 代入②整理,得
代入②整理,得![]() .
.
∴直线![]() 与
与![]() 轴相交于定点
轴相交于定点![]() .
.
(3)当过点![]() 直线
直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,
且![]() ,
, ![]() 在椭圆
在椭圆![]() 上,
上,
由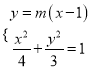 得
得![]() ,易知
,易知![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
,
则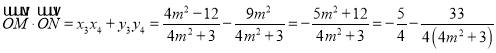 ,
,
∵![]() ,∴
,∴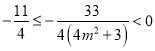 ,
,
∴![]() ,
,
当过点![]() 直线
直线![]() 的斜率不存在时,其方程为
的斜率不存在时,其方程为![]() ,
,
解得![]() ,
, ![]() 或
或![]() ,
, ![]() .
.
此时![]() ,∴
,∴![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目