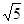题目内容
过双曲线 的一个焦点F引它的渐近线的垂线,垂足为M,延长FM交y轴于E,若|FM|=2|ME|,则该双曲线的离心率为
的一个焦点F引它的渐近线的垂线,垂足为M,延长FM交y轴于E,若|FM|=2|ME|,则该双曲线的离心率为
- A.3
- B.2
- C.

- D.

C
分析:先根据条件求出EF的方程,得到E.F的坐标,再根据|FM|=2|ME|,求出M的坐标,结合点M在渐近线上得到a,b之间的关系,即可求出答案.
解答:渐近线方程是y=± x
x
右焦点的坐标是(c,0)
现在假设由右焦点向一、三象限的渐近线引垂线
所以取方程y= x
x
因为EF垂直于渐近线
所以 直线EF的斜率是-
该直线的方程是y=- (x-c)
(x-c)
当x=0时,y=
所以E点的坐标(0, )
)
∵|FM|=2|ME|,
∴M的坐标( )
)
∵点M在渐近线上,则
整理得:b2=2a2
所以:c2=3a2
∴c= a.
a.
所以离心率e= =
= .
.
故答案为 .
.
点评:本题主要考查了双曲线的简单性质.考查了学生转化和化归的数学思想的运用,以及基本的运算能力.
分析:先根据条件求出EF的方程,得到E.F的坐标,再根据|FM|=2|ME|,求出M的坐标,结合点M在渐近线上得到a,b之间的关系,即可求出答案.
解答:渐近线方程是y=±
 x
x右焦点的坐标是(c,0)
现在假设由右焦点向一、三象限的渐近线引垂线
所以取方程y=
 x
x因为EF垂直于渐近线
所以 直线EF的斜率是-

该直线的方程是y=-
 (x-c)
(x-c)当x=0时,y=

所以E点的坐标(0,
 )
)∵|FM|=2|ME|,
∴M的坐标(
 )
)∵点M在渐近线上,则

整理得:b2=2a2
所以:c2=3a2
∴c=
 a.
a.所以离心率e=
 =
= .
.故答案为
 .
.点评:本题主要考查了双曲线的简单性质.考查了学生转化和化归的数学思想的运用,以及基本的运算能力.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 的一个焦点F作它的一条渐近线的垂线FM,垂足为M并且交
的一个焦点F作它的一条渐近线的垂线FM,垂足为M并且交 轴于E,若M为EF中点,则
轴于E,若M为EF中点,则 =___________.
=___________. 的一个焦点F作一条渐近线的垂线,若垂足恰在线段
的一个焦点F作一条渐近线的垂线,若垂足恰在线段 (
( 为原点)的垂直平分线上,则双曲线的离心率为
.
为原点)的垂直平分线上,则双曲线的离心率为
. 的一个焦点F作其一条渐近线的垂线,若垂足恰在线段OF(O为原点)的垂直平分线上,则双曲线的离心率为( )
的一个焦点F作其一条渐近线的垂线,若垂足恰在线段OF(O为原点)的垂直平分线上,则双曲线的离心率为( ) C.
C. D.
D.
 的一个焦点F作一条渐近线的垂线,若垂足恰在线段
的一个焦点F作一条渐近线的垂线,若垂足恰在线段 (
( 为原点)的垂直平分线上,则双曲线的离心率为_______
___.
为原点)的垂直平分线上,则双曲线的离心率为_______
___. 的一个焦点F作一条渐近的垂线,垂足为点A,与另一条渐近线并于点B,若
的一个焦点F作一条渐近的垂线,垂足为点A,与另一条渐近线并于点B,若 ,则此双曲线的离心率为( )
,则此双曲线的离心率为( )  B.
B. C.2 D.
C.2 D.