题目内容
已知函数y=x+ 有如下性质:如果常数a>0,那么该函数在(0,
有如下性质:如果常数a>0,那么该函数在(0, ]上是减函数,在[
]上是减函数,在[ ,+∞)上是增函数.
,+∞)上是增函数.
(1)如果函数y=x+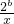 (x>0)的值域为[6,+∞),求b的值;
(x>0)的值域为[6,+∞),求b的值;
(2)研究函数y=x2+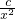 (常数c>0)在定义域内的单调性,并说明理由;
(常数c>0)在定义域内的单调性,并说明理由;
(3)对函数y=x+ 和y=x2+
和y=x2+ (常数a>0)作出推广,使它们都是你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必证明).
(常数a>0)作出推广,使它们都是你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必证明).
解:(1)由函数y=x+ 性质知:
性质知:
当x= 时,函数y=x+
时,函数y=x+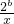 (x>0)的最小值是2
(x>0)的最小值是2 ,则2
,则2 =6,
=6,
解得b=log29.
(2)设0<x1<x2,
则y2-y1= =
= .
.
当 <x1<x2时,y2>y1,函数y=
<x1<x2时,y2>y1,函数y= 在[
在[ ,+∞)上是增函数;
,+∞)上是增函数;
当0<x1<x2< 时,y2<y1,函数y=
时,y2<y1,函数y= 在(0,
在(0, ]上是减函数.
]上是减函数.
又y= 是偶函数,
是偶函数,
所以该函数在(-∞,- ]上是减函数,在[-
]上是减函数,在[- ,0)上是增函数;
,0)上是增函数;
(3)可以把函数推广为y= (常数a>0),其中n是正整数.
(常数a>0),其中n是正整数.
当n是奇数时,函数y= 在(0,
在(0,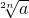 ]上是减函数,在[
]上是减函数,在[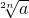 ,+∞)上是增函数,
,+∞)上是增函数,
在(-∞,-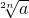 ]上是增函数,在[-
]上是增函数,在[-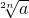 ,0)上是减函数;
,0)上是减函数;
当n是偶数时,函数y= 在(0,
在(0,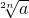 ]上是减函数,在[
]上是减函数,在[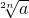 ,+∞) 上是增函数,
,+∞) 上是增函数,
在(-∞,-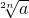 ]上是减函数,在[-
]上是减函数,在[-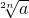 ,0)上是增函数.
,0)上是增函数.
分析:(1)由函数y=x+ 性质可得y=x+
性质可得y=x+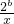 的最小值,令其为6,解出可得b值;
的最小值,令其为6,解出可得b值;
(2)利用定义进行判断:先研究函数在(0,+∞)上的单调性,设0<x1<x2,通过作差判断y2与y1的大小,由单调性的定义即可作出判断,再由偶函数的性质可知函数在(-∞,0)的单调性;
(3)可以把函数推广为y= (常数a>0),其中n是正整数,当n是奇数时类比y=x+
(常数a>0),其中n是正整数,当n是奇数时类比y=x+ 的情形,当n是偶数时类比y=
的情形,当n是偶数时类比y= 的情形,即可得到结论;
的情形,即可得到结论;
点评:本题考查函数单调性的判断、证明及归纳推理,定义是判断函数单调性的基本方法,要熟练掌握.
 性质知:
性质知:当x=
 时,函数y=x+
时,函数y=x+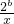 (x>0)的最小值是2
(x>0)的最小值是2 ,则2
,则2 =6,
=6,解得b=log29.
(2)设0<x1<x2,
则y2-y1=
 =
= .
.当
 <x1<x2时,y2>y1,函数y=
<x1<x2时,y2>y1,函数y= 在[
在[ ,+∞)上是增函数;
,+∞)上是增函数;当0<x1<x2<
 时,y2<y1,函数y=
时,y2<y1,函数y= 在(0,
在(0, ]上是减函数.
]上是减函数.又y=
 是偶函数,
是偶函数,所以该函数在(-∞,-
 ]上是减函数,在[-
]上是减函数,在[- ,0)上是增函数;
,0)上是增函数;(3)可以把函数推广为y=
 (常数a>0),其中n是正整数.
(常数a>0),其中n是正整数.当n是奇数时,函数y=
 在(0,
在(0,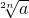 ]上是减函数,在[
]上是减函数,在[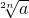 ,+∞)上是增函数,
,+∞)上是增函数,在(-∞,-
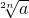 ]上是增函数,在[-
]上是增函数,在[-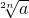 ,0)上是减函数;
,0)上是减函数;当n是偶数时,函数y=
 在(0,
在(0,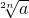 ]上是减函数,在[
]上是减函数,在[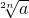 ,+∞) 上是增函数,
,+∞) 上是增函数,在(-∞,-
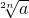 ]上是减函数,在[-
]上是减函数,在[-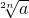 ,0)上是增函数.
,0)上是增函数.分析:(1)由函数y=x+
 性质可得y=x+
性质可得y=x+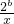 的最小值,令其为6,解出可得b值;
的最小值,令其为6,解出可得b值;(2)利用定义进行判断:先研究函数在(0,+∞)上的单调性,设0<x1<x2,通过作差判断y2与y1的大小,由单调性的定义即可作出判断,再由偶函数的性质可知函数在(-∞,0)的单调性;
(3)可以把函数推广为y=
 (常数a>0),其中n是正整数,当n是奇数时类比y=x+
(常数a>0),其中n是正整数,当n是奇数时类比y=x+ 的情形,当n是偶数时类比y=
的情形,当n是偶数时类比y= 的情形,即可得到结论;
的情形,即可得到结论;点评:本题考查函数单调性的判断、证明及归纳推理,定义是判断函数单调性的基本方法,要熟练掌握.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 (2012•武昌区模拟)已知点P在半径为1的半圆周上沿着A→P→B路径运动,设弧 的长度为x,弓形面积为f(x)(如图所示的阴影部分),则关于函数y=f(x)的有如下结论:
(2012•武昌区模拟)已知点P在半径为1的半圆周上沿着A→P→B路径运动,设弧 的长度为x,弓形面积为f(x)(如图所示的阴影部分),则关于函数y=f(x)的有如下结论: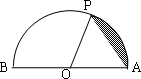
 已知点P在半径为1的半圆周上沿着A→P→B路径运动,设弧 的长度为x,弓形面积为f(x)(如图所示的阴影部分),则关于函数y=f(x)的有如下结论:
已知点P在半径为1的半圆周上沿着A→P→B路径运动,设弧 的长度为x,弓形面积为f(x)(如图所示的阴影部分),则关于函数y=f(x)的有如下结论: