题目内容
7.过抛物线y2=2px(p>0)的焦点F作直线与抛物线交于A,B两点,若以AB为直径的圆与直线x=-1相切,则抛物线的方程为y2=4x.分析 判断以AB为直径的圆与抛物线的准线相切,由已知得准线方程为x=-2,即可求抛物线的标准方程.
解答 解:取AB的中点M,分别过A、B、M作准线的垂线AP、BQ、MN,垂足分别为P、Q、N,如图所示:
由抛物线的定义可知,|AP|=|AF|,|BQ|=|BF|,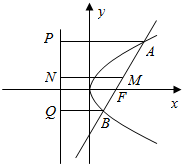
在直角梯形APQB中,|MN|=$\frac{1}{2}$(|AP|+|BQ|)=$\frac{1}{2}$(|AF|+|BF|)=$\frac{1}{2}$|AB|,
故圆心M到准线的距离等于半径,
∴以AB为直径的圆与抛物线的准线相切
由已知得准线方程为x=-1,
∴$\frac{p}{2}$=1,∴p=2,
故所求的抛物线方程为y2=4x.
故答案为:y2=4x.
点评 本题考查直线与抛物线的位置关系、直线圆的位置关系,考查抛物线的定义,考查数形结合思想,属中档题.

练习册系列答案
相关题目