题目内容
7.已知定义在R上的函数f(x)=2|x-m|-1(m为实数)为偶函数,记a=f(log0.53),b=f(log25),c=f(2m),则a,b,c的大小关系为( )| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
分析 根据f(x)为偶函数便可求出m=0,从而f(x)=2|x|-1,这样便知道f(x)在[0,+∞)上单调递增,根据f(x)为偶函数,便可将自变量的值变到区间[0,+∞)上:a=f(|log0.53|),b=f(log25),c=f(0),然后再比较自变量的值,根据f(x)在[0,+∞)上的单调性即可比较出a,b,c的大小.
解答 解:∵f(x)为偶函数;
∴f(-x)=f(x);
∴2|-x-m|-1=2|x-m|-1;
∴|-x-m|=|x-m|;
(-x-m)2=(x-m)2;
∴mx=0;
∴m=0;
∴f(x)=2|x|-1;
∴f(x)在[0,+∞)上单调递增,并且a=f(|log0.53|)=f(log23),b=f(log25),c=f(0);
∵0<log23<log25;
∴c<a<b.
故选:C.
点评 考查偶函数的定义,指数函数的单调性,对于偶函数比较函数值大小的方法就是将自变量的值变到区间[0,+∞)上,根据单调性去比较函数值大小.对数的换底公式的应用,对数函数的单调性,函数单调性定义的运用.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
15.投篮测试中,每人投3次,至少投中2次才能通过测试.己知某同学每次投篮投中的概率为0.6,且各次投篮是否投中相互独立,则该同学通过测试的概率为( )
| A. | 0.648 | B. | 0.432 | C. | 0.36 | D. | 0.312 |
19.若非零向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=$\frac{{2\sqrt{2}}}{3}$|$\overrightarrow{b}$|,且($\overrightarrow{a}$-$\overrightarrow{b}$)⊥(3$\overrightarrow{a}$+2$\overrightarrow{b}$),则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{3π}{4}$ | D. | π |
16.“x=1”是“x2-2x+1=0”的( )
| A. | 充要条件 | B. | 充分而不必要条件 | ||
| C. | 必要而不充分条件 | D. | 既不充分也不必要条件 |
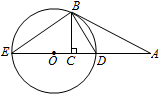 如图,AB切⊙O于点B,直线AO交⊙O于D,E两点,BC⊥DE,垂足为C.
如图,AB切⊙O于点B,直线AO交⊙O于D,E两点,BC⊥DE,垂足为C. 如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点A(0,-1),且离心率为$\frac{\sqrt{2}}{2}$.
如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点A(0,-1),且离心率为$\frac{\sqrt{2}}{2}$.