题目内容
已知F1,F2为双曲线C: 的左右焦点,点P在C上,
的左右焦点,点P在C上, ,则
,则 ( )
( )
| A.2 | B.4 | C. 6 | D. 8 |
B
解析试题分析:在 中,
中, ,
, ,
, …………①
…………①
由余弦定理得:
 ,即
,即

 …………………②
…………………②
把①代入②得: 4.
4.
考点:本题考查双曲线的简单性质,余弦定理。
点评:圆锥曲线上一点与其两焦点所构成的三角形叫做圆锥曲线的焦点三角形。焦点三角形在我们做题时经常见到。当见到焦点三角形的时候一般要联系余弦定理、圆锥曲线的定义来解决。

练习册系列答案
相关题目
抛物线 的准线方程是
的准线方程是 ,则
,则 的值为 ( )
的值为 ( )
| A.4 | B. | C. | D.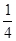 |
若直线 和⊙O:
和⊙O: 没有交点,则过
没有交点,则过 的直线与椭圆
的直线与椭圆 的交点个数 ( )
的交点个数 ( )
| A.至多一个 | B.0个 | C.1个 | D.2个 |
已知椭圆 和双曲线
和双曲线 ,有相同的焦点,则椭圆与双曲线的离心率的平方和为( )
,有相同的焦点,则椭圆与双曲线的离心率的平方和为( )
A. | B. | C.2 | D.3 |
如图,把椭圆 的长轴
的长轴 分成
分成 等份,过每个分点作
等份,过每个分点作 轴的垂线交椭圆的上半部分于
轴的垂线交椭圆的上半部分于 七个点,
七个点, 是椭圆的一个焦点,则
是椭圆的一个焦点,则 ( )
( )
| A.28 | B.30 | C.35 | D.25 |
 的左顶点A的斜率为k的直线交椭圆C于另一个点B,且点B在x轴上的射影恰好为右焦点F,若
的左顶点A的斜率为k的直线交椭圆C于另一个点B,且点B在x轴上的射影恰好为右焦点F,若 则椭圆离心率的取值范围是( )
则椭圆离心率的取值范围是( )



 的两个焦点,过F2的直线交椭圆于点A、B,若
的两个焦点,过F2的直线交椭圆于点A、B,若 ,则
,则 ( )
( ) 的左、右焦点分别为F1、F2,线段F1F2被抛物线y2=2bx的焦点分成5:3两段,则此椭圆的离心率为 ( )
的左、右焦点分别为F1、F2,线段F1F2被抛物线y2=2bx的焦点分成5:3两段,则此椭圆的离心率为 ( )



 的焦点与椭圆
的焦点与椭圆 的一个焦点重合,过点
的一个焦点重合,过点 的直线与抛物线交于
的直线与抛物线交于 两点,若
两点,若 ,则
,则 的值( )
的值( )

