题目内容
(本小题14分)已知函数 ,且
,且
(1)求 的值;
的值;
(2)判断函数 在
在 上是增函数还是减函数?并证明.
上是增函数还是减函数?并证明.
(1)2;(2)增函数.
【解析】
试题分析:(1)待定系数法求 的值;(2)根据增、减函数的定义,任取
的值;(2)根据增、减函数的定义,任取 ,不妨设
,不妨设 ,,利用作差法若证明出
,,利用作差法若证明出 ,则函数为增函数,若证明出
,则函数为增函数,若证明出 ,则函数为减函数.
,则函数为减函数.
试题解析:(1)
(2)函数 在
在 上是增函数,证明如下:
上是增函数,证明如下:
任取 ,不妨设
,不妨设 ,
, 

 且
且


即 ,函数
,函数 在
在 上是增函数
上是增函数
考点:1、待定系数法;2、证明函数的单调性.

练习册系列答案
相关题目
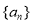 是等差数列,
是等差数列, 为等比数列,其公比q≠1, 且
为等比数列,其公比q≠1, 且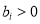 (i=1、2、3 …n)若
(i=1、2、3 …n)若 ,
,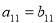 则
则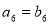 B.
B.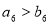
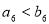 D.
D.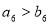 或
或 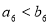
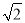 的等腰直角三角形,则该三棱锥的外接球的表面积是( )
的等腰直角三角形,则该三棱锥的外接球的表面积是( )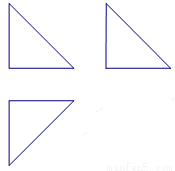
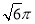 (B)6
(B)6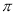 (C)
(C)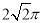 (D)
(D)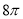
 ,若
,若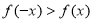 ,则x的取值范围是
,则x的取值范围是 ,
, ,则
,则
 若
若 .
.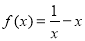 的图像关于( )
的图像关于( )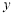 轴对称 B. 直线
轴对称 B. 直线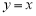 对称 C. 坐标原点对称 D. 直线
对称 C. 坐标原点对称 D. 直线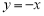 对称
对称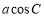 ,
,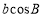 ,
,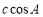 满足
满足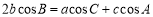 ,若
,若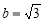 ,则
,则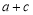 的最大值为
的最大值为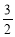 B.3 C.
B.3 C.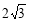 D.9
D.9 的焦点到它的准线的距离等于 .
的焦点到它的准线的距离等于 .