题目内容
已知函数f(x)=x2+ax+b(其中a,b∈R),(1)若当x∈[-1,1],f(x)≤0恒成立,求
 的取值范围;
的取值范围;(2)若a∈[-1,1],b∈[-1,1],求f(x)无零点的概率;
(3)若对于任意的正整数k,当
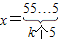 时,都有
时,都有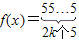 成立,则称这样f(x)是K2函数,现有函数
成立,则称这样f(x)是K2函数,现有函数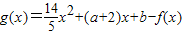 ,试判断g(x)是不是K2函数?并给予证明.?
,试判断g(x)是不是K2函数?并给予证明.?
【答案】分析:(1)据f(x)≤0恒成立,由有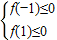 得到
得到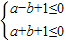 ,再观察
,再观察 的结构形式,可用线性规划解决;
的结构形式,可用线性规划解决;
(2)据a∈[-1,1],b∈[-1,1],可知这是一个几何概型中的面积类型,总面积是直线a=±1,b=±1围成的区域面积,当f(x)有零点时,则判断式大于零,得到a2≥4b,满足条件为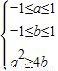 ,可用定积分求得有零点时的面积,从而求得有零 点时的概率,再用对立事件求得无零点时的概率;
,可用定积分求得有零点时的面积,从而求得有零 点时的概率,再用对立事件求得无零点时的概率;
(3)g(x)是K2函数,按照定义证明即可.
解答:解:(1)据题意: ∴
∴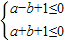
可行域如图 的几何意义是定点P(2,5)到区域内的点Q(a,b)连线的斜率k,
的几何意义是定点P(2,5)到区域内的点Q(a,b)连线的斜率k,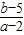 的取值范围为(-∞,-1)∪(1,+∞);
的取值范围为(-∞,-1)∪(1,+∞);
(2)当f(x)有零点时,a2≥4b,满足条件为
由抛物线的下方与a=±1,b=-1围成的区域面积,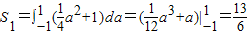 ,
,
由直线a=±1,b=±1围成的区域面积S2=4,
故f(x)有零点的概率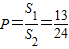 ,∴f(x)无零点的概率为
,∴f(x)无零点的概率为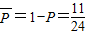 ;
;
(3)g(x)是K2函数,
证明: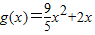 符合条件,
符合条件,
因为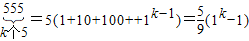 ,
,
同理: ;
;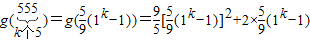
=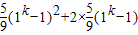 =
=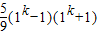 =
=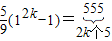 ,
,
所以, 符合条件.
符合条件.
点评:本题主要考查线性规划,(1)关键是确定约束条件和目标函数类型;(2)是结合概率来考查所围成的平面图形的面积;(3)是情境题,这样题的解决要严格执行给定的定义,结合已有的知识解决.
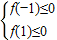 得到
得到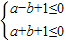 ,再观察
,再观察 的结构形式,可用线性规划解决;
的结构形式,可用线性规划解决;(2)据a∈[-1,1],b∈[-1,1],可知这是一个几何概型中的面积类型,总面积是直线a=±1,b=±1围成的区域面积,当f(x)有零点时,则判断式大于零,得到a2≥4b,满足条件为
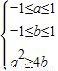 ,可用定积分求得有零点时的面积,从而求得有零 点时的概率,再用对立事件求得无零点时的概率;
,可用定积分求得有零点时的面积,从而求得有零 点时的概率,再用对立事件求得无零点时的概率; (3)g(x)是K2函数,按照定义证明即可.
解答:解:(1)据题意:
 ∴
∴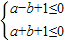
可行域如图
 的几何意义是定点P(2,5)到区域内的点Q(a,b)连线的斜率k,
的几何意义是定点P(2,5)到区域内的点Q(a,b)连线的斜率k,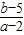 的取值范围为(-∞,-1)∪(1,+∞);
的取值范围为(-∞,-1)∪(1,+∞);(2)当f(x)有零点时,a2≥4b,满足条件为

由抛物线的下方与a=±1,b=-1围成的区域面积,
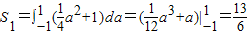 ,
,由直线a=±1,b=±1围成的区域面积S2=4,
故f(x)有零点的概率
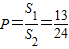 ,∴f(x)无零点的概率为
,∴f(x)无零点的概率为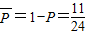 ;
;(3)g(x)是K2函数,
证明:
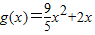 符合条件,
符合条件,因为
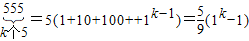 ,
,同理:
 ;
;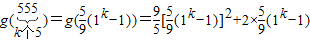
=
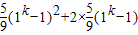 =
=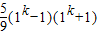 =
=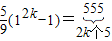 ,
,所以,
 符合条件.
符合条件.点评:本题主要考查线性规划,(1)关键是确定约束条件和目标函数类型;(2)是结合概率来考查所围成的平面图形的面积;(3)是情境题,这样题的解决要严格执行给定的定义,结合已有的知识解决.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|