题目内容
(1)设90°<α<180°,角α的终边上一点为P(x, ),且cosα=
),且cosα= x,求sinα与tanα的值;
x,求sinα与tanα的值;
(2)已知角θ的终边上有一点P(x,-1)(x≠0),且tanθ=-x,求sinθ,cosθ.
解:(1)由题意知,r= ,∴cosα=
,∴cosα= ,
,
∴ x=
x= ,解得x=0或x=±
,解得x=0或x=± .
.
∵90°<α<180°,∴x<0,因此x=- .
.
故r=2 ,sinα=
,sinα= =
=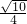 ,
,
tanα= =-
=- .
.
(2)∵θ的终边过点(x,-1),∴tanθ=- ,
,
又∵tanθ=-x,∴x2=1,解得x=±1.
当x=1时,sinθ=- ,cosθ=
,cosθ= ;
;
当x=-1时,sinθ=- ,cosθ=-
,cosθ=- .
.
分析:(1)由题意求点P和原点之间的距离r= ,再由余弦函数的定义列出方程,求出x的值,再根据角的范围确定x的值,再根据任意角的三角函数定义求出sinα与tanα的值;
,再由余弦函数的定义列出方程,求出x的值,再根据角的范围确定x的值,再根据任意角的三角函数定义求出sinα与tanα的值;
(2)根据正切函数的定义,列出方程求出x的值,因x的值有两个故分两种情况,根据任意角的三角函数定义求出sinθ,cosθ的值.
点评:本题考查了任意角的三角函数定义,即由角的终边上的一点坐标表示出该角的三角函数值.
 ,∴cosα=
,∴cosα= ,
,∴
 x=
x= ,解得x=0或x=±
,解得x=0或x=± .
.∵90°<α<180°,∴x<0,因此x=-
 .
.故r=2
 ,sinα=
,sinα= =
=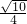 ,
,tanα=
 =-
=- .
.(2)∵θ的终边过点(x,-1),∴tanθ=-
 ,
,又∵tanθ=-x,∴x2=1,解得x=±1.
当x=1时,sinθ=-
 ,cosθ=
,cosθ= ;
;当x=-1时,sinθ=-
 ,cosθ=-
,cosθ=- .
.分析:(1)由题意求点P和原点之间的距离r=
 ,再由余弦函数的定义列出方程,求出x的值,再根据角的范围确定x的值,再根据任意角的三角函数定义求出sinα与tanα的值;
,再由余弦函数的定义列出方程,求出x的值,再根据角的范围确定x的值,再根据任意角的三角函数定义求出sinα与tanα的值;(2)根据正切函数的定义,列出方程求出x的值,因x的值有两个故分两种情况,根据任意角的三角函数定义求出sinθ,cosθ的值.
点评:本题考查了任意角的三角函数定义,即由角的终边上的一点坐标表示出该角的三角函数值.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
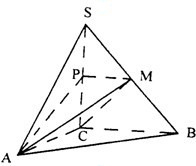 如图,在三棱锥S-ABC中,SC⊥平面ABC,点P、M分别是SC和SB的中点,设PM=AC=1,∠ACB=90°,直线AM与直线SC所成的角为60°.
如图,在三棱锥S-ABC中,SC⊥平面ABC,点P、M分别是SC和SB的中点,设PM=AC=1,∠ACB=90°,直线AM与直线SC所成的角为60°. 在直三棱柱ABC-A1B1C1中,AB=AC=1,∠BAC=90°,且异面直线A1B与B1C1所成的角等于60°,设AA1=a.
在直三棱柱ABC-A1B1C1中,AB=AC=1,∠BAC=90°,且异面直线A1B与B1C1所成的角等于60°,设AA1=a. ),且cosα=
),且cosα= x,求sinα与tanα的值;
x,求sinα与tanα的值;