题目内容
已知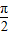 <β<α<
<β<α<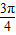 ,cos(α-β)=
,cos(α-β)=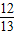 ,sin(α+β)=-
,sin(α+β)=- ,求sin2α的值 .
,求sin2α的值 .
【答案】分析:由α-β的余弦值和α、β角的范围求出α-β的正弦值,由α+β的正弦值和范围,求出α+β的余弦值,要求的结论2α的正弦值,把2α变化为(α-β)+(α+β)的正弦值求解.
解答:解:∵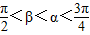 ,
,
∴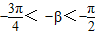
∴0<α-β<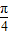
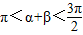
∴sin(α-β)=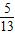
cos(α+β)=-
∴sin2α=sin【(α-β)+(α+β)】=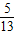 ×(
×(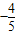 )+
)+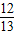 ×(
×(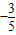 )=
)=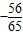 ,
,
故答案为:-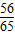
点评:已知一个角的某个三角函数式的值,求这个角的其他三角函数式的值,一般需用三个基本关系式及其变式,通过恒等变形或解方程求解,本题是给值求值,但是本题主要考查角的变换,遇到这种问题我们一般整体处理题目条件,而不能分解.
解答:解:∵
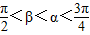 ,
,∴
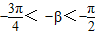
∴0<α-β<
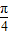
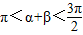
∴sin(α-β)=
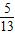
cos(α+β)=-

∴sin2α=sin【(α-β)+(α+β)】=
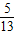 ×(
×(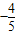 )+
)+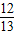 ×(
×(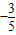 )=
)=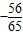 ,
,故答案为:-
点评:已知一个角的某个三角函数式的值,求这个角的其他三角函数式的值,一般需用三个基本关系式及其变式,通过恒等变形或解方程求解,本题是给值求值,但是本题主要考查角的变换,遇到这种问题我们一般整体处理题目条件,而不能分解.

练习册系列答案
相关题目
 如图,已知O为△ABC的外心,a,b,c分别是角A、B、C的对边,且满足
如图,已知O为△ABC的外心,a,b,c分别是角A、B、C的对边,且满足