题目内容
如图，在平行六面体ABCD-A1B1C1D1中，AB=5，AD=3，AA1=4，∠DAB=90°，∠BAA1=∠DAA1=60°，E是CC1的中点，设| AB |
| a |
| AD |
| b |
| AA1 |
| c |
（1）用
| a |
| b |
| c |
| AE |
（2）求AE的长？
分析：（1）根据向量的三角形法则把要表示的向量写成以几何体的棱为基底的向量的加法的形式，从向量的起点出发，沿着棱到终点．
（2）根据上一问表示出的结果，把要求的向量两边平方，把得到平方式展开，得到已知向量的模长和数量积的关系，代入数据做出结果．
（2）根据上一问表示出的结果，把要求的向量两边平方，把得到平方式展开，得到已知向量的模长和数量积的关系，代入数据做出结果．
解答：解：（1）根据向量的三角形法则得到
=
+
+
=
+
+
（2）∵|
|2=(
+
+
)2
=
2+
2+
2+2
•
+
•
+
•
=25+9+4+0+（20+12）•cos60°
=54
∴|
|=3
，
即AE的长为3
．
| AE |
| AB |
| BC |
| CE |
| a |
| b |
| 1 |
| 2 |
| c |
（2）∵|
| AE |
| a |
| b |
| 1 |
| 2 |
| c |
=
| a |
| b |
| 1 |
| 4 |
| c |
| a |
| b |
| a |
| c |
| b |
| c |
=25+9+4+0+（20+12）•cos60°
=54
∴|
| AE |
| 6 |
即AE的长为3
| 6 |
点评：本题考查向量的基底表示和向量的模长的计算，本题解题的关键是把要求模长的向量表示成已知模长和夹角的向量的形式的运算．
练习册系列答案
名校课堂系列答案
相关题目
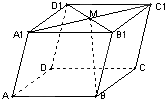如图：在平行六面体ABCD-A1B1C1D1中，M为A1C1与B1D1的交点．若| AB |
| a |
| AD |
| b |
| AA1 |
| c |
| BM |
A、-
| ||||||||||
B、
| ||||||||||
C、-
| ||||||||||
D、
|
如图，在平行六面体ABCD-A1B1C1D1中，已知| AB |
| AD |
| AA1 |
| a |
| b |
| c |
| BD1 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、-
|
对于向量a，b，定义a×b为向量a，b的向量积，其运算结果为一个向量，且规定a×b的模|a×b|=|a||b|sinθ（其中θ为向量a与b的夹角），a×b的方向与向量a，b的方向都垂直，且使得a，b，a×b依次构成右手系．如图，在平行六面体ABCD-EFGH中，∠EAB=∠EAD=∠BAD=60°，AB=AD=AE=2，则
如图，在平行六面体ABCD-A1B1C1D1中，若| AB |
| a |
| AD |
| b |
| AA1 |
| c |
| D1B |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、-
|
（2001•上海）如图，在平行六面体ABCD-A1B1C1D1中，M为AC与BD的交点，若