题目内容
(本小题共14分)
在如图的多面体中,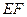 ⊥平面
⊥平面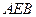 ,
,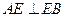 ,
,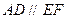 ,
,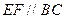 ,
,
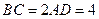 ,
,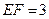 ,
,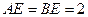 ,
, 是
是 的
的 中点.
中点.
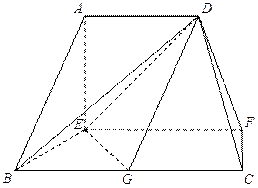
(Ⅰ) 求证: 平面
平面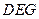 ;
;
(Ⅱ) 求证: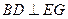 ;
;
(Ⅲ) 求二面角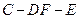 的余弦值.
的余弦值.
在如图的多面体中,
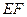 ⊥平面
⊥平面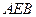 ,
,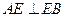 ,
,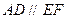 ,
,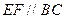 ,
,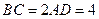 ,
,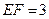 ,
,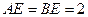 ,
,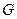 是
是 的
的 中点.
中点.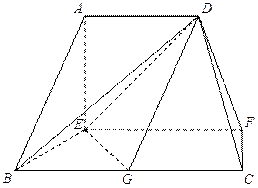
(Ⅰ) 求证:
 平面
平面 ;
;(Ⅱ) 求证:
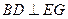 ;
;(Ⅲ) 求二面角
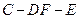 的余弦值.
的余弦值. 
解:(Ⅰ)证明:∵
 ,
,∴
 .
.又∵
 ,
,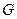 是
是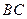 的中点,
的中点,∴
 ,
,∴四边形
 是平行四边形,
是平行四边形, ∴
∴  . ……………2分
. ……………2分∵
 平面
平面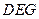 ,
, 平面
平面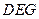 ,
,∴
 平面
平面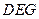 .
.  …………………4分
…………………4分
∴四边形
 为正方形,
为正方形,∴
 , ………………………7分
, ………………………7分又
 平面
平面 ,
, 平面
平面 ,
,∴
 ⊥平面
⊥平面 . ……………………8分
. ……………………8分∵
 平面
平面 ,
,∴
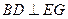 . ………………………9分
. ………………………9分解法2
∵
 平面
平面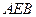 ,
, 平面
平面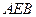 ,
, 平
平 面
面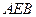 ,∴
,∴ ,
, ,
,又
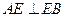 ,
,∴
 两两垂直. ……………………5分
两两垂直. ……………………5分以点E为坐标原点,
 分别为
分别为 轴建立如图的空间直角坐标系.
轴建立如图的空间直角坐标系.由已知得,
 (0,0,2),
(0,0,2), (2,0,0),
(2,0,0), (2,4,0),
(2,4,0), (0,3,0),
(0,3,0), (0,2,2),
(0,2,2),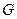 (2,2,0). …………………………6分
(2,2,0). …………………………6分∴
 ,
, ,………7分
,………7分∴
 , ………8分
, ………8分∴
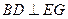 . …………………………9分
. …………………………9分
略

练习册系列答案
相关题目
 中,AB=1,
中,AB=1,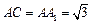 ,
,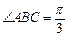 .
.
 ;
;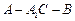 的正弦值.
的正弦值.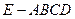 中,底面
中,底面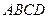 为正方形,
为正方形,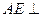 平面
平面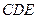 ,已知
,已知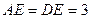 ,
, 为线段
为线段 上的动点.
上的动点.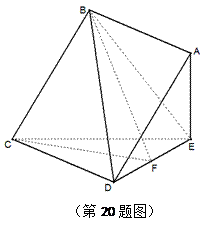
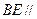 平面
平面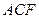 ;
;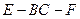 与二面角
与二面角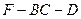 的大小相等,求
的大小相等,求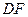 长.
长.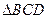 与
与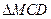 都是边长为2的正三角形,平面
都是边长为2的正三角形,平面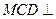 平面
平面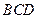 ,
,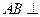 平面BCD,
平面BCD,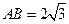 .求点A到平面MBC的距离。
.求点A到平面MBC的距离。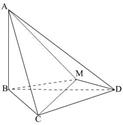
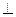 BC,AC=BC=4,四边形ABDE是直角梯形,BD
BC,AC=BC=4,四边形ABDE是直角梯形,BD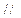 AE,BD
AE,BD
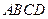 中,
中,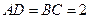 ,
,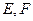 分别是
分别是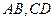 的中点,
的中点,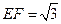 ,求异面直线
,求异面直线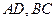 所成的角.
所成的角.
