Question

（2012•合肥一模）在正四面体的6条棱中随机抽取2条，则其2条棱互相垂直的概率为（　　）

• A．

  3

  4

• B．

  2

  3

• C．

  1

  5

• D．

  1

  3

Answer 1

分析：根据题意，作出正四面体A-BCD，由组合数公式可得从其6条棱中随机抽取2条的取法数目，结合正四面体的几何结构分析可得其相互垂直的棱的数目，由等可能事件的概率公式，计算可得答案．

解答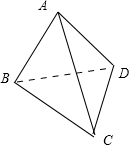：解：根据题意，如右图，在正四面体A-BCD的6条棱中随机抽取2条，有C₆²=15种情况，
又由正四面体的几何结构，其中相互垂直的棱有AC、BD，AB、CD，AD、BC，共3组，
则其概率P=

3

15

=

1

5

；
故选C．

点评：本题考查等可能事件的概率以及正四面体的几何结构，关键是由正四面体的几何结构得到相互垂直的棱的数目．