题目内容
8.与直线x+y-2=0和圆x2+y2-12x-12y+54=0都相切的半径最小的圆的方程.分析 由题意可知先求圆心坐标,再求圆心到直线的距离,求出最小的圆的半径,圆心坐标,可得圆的方程.
解答 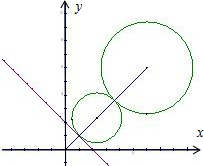 解:圆x2+y2-12x-12y+54=0化为(x-6)2+(y-6)2=18,
解:圆x2+y2-12x-12y+54=0化为(x-6)2+(y-6)2=18,
其圆心到直线x+y-2=0的距离为d=$\frac{|6+6-2|}{\sqrt{2}}$=5$\sqrt{2}$.
所求的最小圆的圆心在直线y=x上,
其到直线的距离为$\sqrt{2}$,圆心坐标为(2,2).
标准方程为(x-2)2+(y-2)2=2.
点评 本题考查直线和圆的方程的应用,考查转化的数学思想,是中档题.

练习册系列答案
相关题目
13.一对父子参加一个亲子摸奖游戏,其规则如下:父亲在装有红色、白色球各两个的甲袋子里随机取两个球,儿子在装有红色、白色、黑色球各一个的乙袋子里随机取一个球,父子俩取球相互独立,两人各摸球一次合在一起称为一次摸奖,他们取出的三个球的颜色情况与他们获得的积分对应如下表:
(Ⅰ)求一次摸奖中,所取的三个球中恰有两个是红球的概率;
(Ⅱ)设一次摸奖中,他们所获得的积分为X,求X的分布列及均值(数学期望)E(X).
| 所取球的情况 | 三个球均为红色 | 三个球均不同色 | 恰有两球为红色 | 其他情况 |
| 所获得的积分 | 180 | 90 | 60 | 0 |
(Ⅱ)设一次摸奖中,他们所获得的积分为X,求X的分布列及均值(数学期望)E(X).
17.关于x的不等式x2-bx+c<0的解集为(-1,2),则方程x2-bx+2c=0的两根之积为( )
| A. | -4 | B. | -2 | C. | 2 | D. | 4 |
18.有一个长为1km的斜坡,它的倾斜角为75°,现要将其倾斜角改为30°,则坡底要伸长( )
| A. | 1km | B. | $\sqrt{2}$km | C. | $\sqrt{3}$km | D. | 2km |