题目内容
(1) 给定正整数n![]() 5,集合 An=
5,集合 An=![]() .是否存在一一映射
.是否存在一一映射 ![]() : An
: An![]() An满足条件:对一切k ( 1
An满足条件:对一切k ( 1![]() k
k ![]() n-1 ) , 都有k |
n-1 ) , 都有k | ![]() (1)+
(1)+![]() (2) +……+
(2) +……+![]() (k) ?
(k) ?
(2) N* 为全体正整数的集合,是否存在一一映射 ![]() : N*
: N*![]() N* 满足条件:对一切k
N* 满足条件:对一切k![]() N*, 都有k |
N*, 都有k | ![]() (1)+
(1)+![]() (2) + ……+
(2) + ……+![]() (k) ?
(k) ?
证明你的结论 .
注: 映射 ![]() : A
: A![]() B 称为一一映射,如果对任意 b
B 称为一一映射,如果对任意 b![]() B,有且只有一个 a
B,有且只有一个 a![]() A 使得
A 使得 ![]() (a)=b . 题中“|”为整除符号.
(a)=b . 题中“|”为整除符号.
解析:(1) 不存在. ( 5 分)记 S k =![]() .当 n = 2m+1 时 ( m
.当 n = 2m+1 时 ( m ![]() 2 ), 由 2m | S 2 m 及S 2 m=
2 ), 由 2m | S 2 m 及S 2 m=![]() -
-![]() (2m+1) 得
(2m+1) 得 ![]() (2m+1)
(2m+1)![]() m+1(mod 2m), 但
m+1(mod 2m), 但 ![]() (2m+1)
(2m+1)![]() A 2m+1,故
A 2m+1,故![]() (2m+1)= m+1.再由 2m-1 | S2m-1及
(2m+1)= m+1.再由 2m-1 | S2m-1及
S2m-1=![]() -(m+1)-
-(m+1)-![]() (2m) 得
(2m) 得![]() (2m)
(2m) ![]() m+1(mod 2m-1),又有
m+1(mod 2m-1),又有![]() (2m)= m+1,与
(2m)= m+1,与![]()
的一一性矛盾. ( 5 分)
当 n = 2m+2 时 ( m![]() 2 ), S2m+1=
2 ), S2m+1=![]() -
-![]() (2m+2) 给出
(2m+2) 给出![]() (2m+2)=1 或 2m+2,
(2m+2)=1 或 2m+2,
同上又得![]() (2m+1)=
(2m+1)= ![]() (2m)= m+2 或 m+1 ,矛盾. ( 5 分)
(2m)= m+2 或 m+1 ,矛盾. ( 5 分)
(2) 存在. 对n 归纳定义![]() (2n-1)及
(2n-1)及![]() (2n) 如下: ( 5 分)
(2n) 如下: ( 5 分)
令![]()
![]() (1)=1,
(1)=1, ![]() (2)=3 .设已定义出不同的正整数值
(2)=3 .设已定义出不同的正整数值![]() (k) (1
(k) (1![]() k
k![]() 2n)满足整除条件且包含 1,2,…,n ,设 v 是未取到的最小正整数值,由于 2n+1 与 2n+2 互素,根据孙子定理,存在不同于v及
2n)满足整除条件且包含 1,2,…,n ,设 v 是未取到的最小正整数值,由于 2n+1 与 2n+2 互素,根据孙子定理,存在不同于v及![]() (k) (1
(k) (1![]() k
k![]() 2n)的正整数u满足同余式组
2n)的正整数u满足同余式组
u![]() -S2n(mod 2n+1)
-S2n(mod 2n+1)![]() -S2n-v (mod 2n+2) . ( 5 分)
-S2n-v (mod 2n+2) . ( 5 分)
定义![]() (2n+1)=u,
(2n+1)=u, ![]() (2n+2)=v .则正整数
(2n+2)=v .则正整数![]() (k) ( 1
(k) ( 1![]() k
k![]() 2n+2 )也互不相同,满足整除条件,且包含
2n+2 )也互不相同,满足整除条件,且包含
1,2,…,n+1 .根据数学归纳法原理,已经得到符合要求的一一映射

 字词句段篇系列答案
字词句段篇系列答案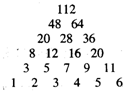 给定正整数n(n≥2)按图方式构成三角形数表:第一行依次写上数1,2,3,…,n,在下面一行的每相邻两个数的正中间上方写上这两个数之和,得到上面一行的数(比下一行少一个数),依此类推,最后一行(第n行)只有一个数.例如n=6时数表如图所示,则当n=2010时最后一行的数是
给定正整数n(n≥2)按图方式构成三角形数表:第一行依次写上数1,2,3,…,n,在下面一行的每相邻两个数的正中间上方写上这两个数之和,得到上面一行的数(比下一行少一个数),依此类推,最后一行(第n行)只有一个数.例如n=6时数表如图所示,则当n=2010时最后一行的数是