题目内容
已知数列![]() 满足
满足![]() ,求数列
,求数列![]() 的通项公式。
的通项公式。
解:设![]()
![]() ⑧
⑧
将![]() 代入⑧式,得
代入⑧式,得
![]()
![]() ,则
,则
![]()
等式两边消去![]() ,得
,得![]() ,
,
则得方程组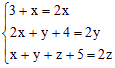 ,则
,则![]() ,代入⑧式,得
,代入⑧式,得
![]()
![]() ⑨
⑨
由![]() 及⑨式,得
及⑨式,得
![]()
则![]() ,故数列
,故数列![]() 为以
为以![]() 为首项,以2为公比的等比数列,因此
为首项,以2为公比的等比数列,因此![]() ,则
,则![]() 。
。
解析:
本题解题的关键是把递推关系式![]() 转化为
转化为![]() ,从而可知数列
,从而可知数列![]() 是等比数列,进而求出数列
是等比数列,进而求出数列![]() 的通项公式,最后再求出数列
的通项公式,最后再求出数列![]() 的通项公式。
的通项公式。

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
题目内容
已知数列![]() 满足
满足![]() ,求数列
,求数列![]() 的通项公式。
的通项公式。
解:设![]()
![]() ⑧
⑧
将![]() 代入⑧式,得
代入⑧式,得
![]()
![]() ,则
,则
![]()
等式两边消去![]() ,得
,得![]() ,
,
则得方程组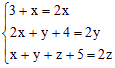 ,则
,则![]() ,代入⑧式,得
,代入⑧式,得
![]()
![]() ⑨
⑨
由![]() 及⑨式,得
及⑨式,得
![]()
则![]() ,故数列
,故数列![]() 为以
为以![]() 为首项,以2为公比的等比数列,因此
为首项,以2为公比的等比数列,因此![]() ,则
,则![]() 。
。
本题解题的关键是把递推关系式![]() 转化为
转化为![]() ,从而可知数列
,从而可知数列![]() 是等比数列,进而求出数列
是等比数列,进而求出数列![]() 的通项公式,最后再求出数列
的通项公式,最后再求出数列![]() 的通项公式。
的通项公式。

 优加精卷系列答案
优加精卷系列答案