题目内容
将棱长为2的正方体木块切削成一个体积最大的球,则该球的体积为( )
分析:根据已知中,将棱长为2的正方体木块切削成一个体积最大的球,结合正方体和圆的结构特征,就是正方体的内切球,我们可以求出球的半径,代入球的体积公式即可求出答案.
解答:解:将棱长为2的正方体木块切削成一个体积最大的球时,
球的直径等于正方体的棱长2,
则球的半径R=1,
则球的体积V=
•π•R3=
故选A.
球的直径等于正方体的棱长2,
则球的半径R=1,
则球的体积V=
| 4 |
| 3 |
| 4π |
| 3 |
故选A.
点评:本题考查的知识点是球的体积,其中根据正方体和圆的结构特征,求出球的半径,是解答本题的关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 B.
B. C.
C.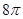 D.
D.
 B.
B. C.
C. D.
D.
