题目内容
以抛物线y2=4px(p>0)的焦点F(1,0)为圆心,且过坐标原点的圆的方程为
(x-1)2+y2=1或x2+y2-2x=0
(x-1)2+y2=1或x2+y2-2x=0
.分析:由抛物线的方程可求得其焦点坐标,结合题意可求得满足条件的圆的方程.
解答:解:∵抛物线的方程为y2=4px(p>0),
∴其焦点坐标为F(1,0),
∴设以焦点F为圆心的圆的方程为:(x-1)2+y2=r2,
∵该圆过坐标原点,
∴12+02=r2,
∴r2=1,
∴所求的圆的方程为:(x-1)2+y2=1,或者写成x2+y2-2x=0.
故答案为:(x-1)2+y2=1或x2+y2-2x=0.
∴其焦点坐标为F(1,0),
∴设以焦点F为圆心的圆的方程为:(x-1)2+y2=r2,
∵该圆过坐标原点,
∴12+02=r2,
∴r2=1,
∴所求的圆的方程为:(x-1)2+y2=1,或者写成x2+y2-2x=0.
故答案为:(x-1)2+y2=1或x2+y2-2x=0.
点评:本题考查抛物线的简单性质,考查圆的标准方程,求得抛物线的焦点是关键,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
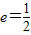 ;且抛物线C1和椭圆C2的一个交点记为M.
;且抛物线C1和椭圆C2的一个交点记为M.