题目内容
17.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,过椭圆C的焦点且垂直于x轴的直线被椭圆C截得的线段长为1.(1)求椭圆C的方程;
(2)过点M(m,0)作圆x2+y2=1的切线l交曲线C于A,B两点,试探究|AB|是否有最大值,若有,求出|AB|的最大值及相应的实数m;若没有,请说明理由.
分析 (1)利用椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,过椭圆C的焦点且垂直于x轴的直线被椭圆C截得的线段长为1,建立方程,求得几何量,即可求得椭圆G的方程;
(2)由题意知,|m|≥1,分类讨论:当m=±1时,|AB|=$\sqrt{3}$;当|m|>1时,设l的方程代入椭圆方程,利用韦达定理,及l与圆x2+y2=1相切,可表示|AB|,利用基本不等式可求最值,从而可得结论.
解答 解:(1)∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,
∴$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,
∵过椭圆C的焦点且垂直于x轴的直线被椭圆C截得的线段长为1,
∴$\frac{2{b}^{2}}{a}$=1,
∴a=2,b=1,
∴椭圆C的方程$\frac{{x}^{2}}{4}$+y2=1;
(2)由题意知,|m|≥1
当m=±1时,切线l的方程为x=±1,此时|AB|=$\sqrt{3}$;
当|m|>1时,设l为y=k(x-m),代入椭圆方程可得(1+4k2)x2-8k2mx+4k2m2-4=0
设A、B的坐标分别为(x1,y1),(x2,y2),则x1+x2=$\frac{8{k}^{2}m}{1+4{k}^{2}}$,x1x2=$\frac{4{k}^{2}{m}^{2}-4}{1+4{k}^{2}}$
∵l与圆x2+y2=1相切,∴$\frac{|km|}{\sqrt{{k}^{2}+1}}$=1,即m2k2=k2+1
∴|AB|=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\frac{4\sqrt{3}|m|}{{m}^{2}+3}$=$\frac{4\sqrt{3}}{|m|+\frac{3}{|m|}}$≤2(当且仅当m=±$\sqrt{3}$时取等号)
∴|AB|的最大值为2,m=±$\sqrt{3}$.
点评 本题考查椭圆的性质与标准方程,考查直线与椭圆的位置关系,考查弦长的计算,考查韦达定理的运用,正确运用韦达定理是关键.

| A. | 30 | B. | 45 | C. | 180 | D. | 720 |
| A. | f(1)>e,f(2012)>e2012 | B. | f(1)>e,f(2012)<e2012 | ||
| C. | f(1)<e,f(2012)>e2012 | D. | f(1)<e,f(2012)<e2012 |
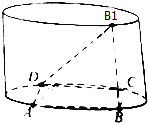 如图,圆柱底面直径为10,母线BB1=6,矩形ABCD内接于圆柱的下底面,BC=6,求直线DB1与BC所成角的大小.(结果用反三角函教值表示)
如图,圆柱底面直径为10,母线BB1=6,矩形ABCD内接于圆柱的下底面,BC=6,求直线DB1与BC所成角的大小.(结果用反三角函教值表示)