题目内容
20．已知双曲线$\frac{x^2}{36}-\frac{y^2}{64}=1$上一点P到双曲线的一个焦点距离为15，则点P到另外一个焦点的距离为（ ）| A． | 3或27 | B． | 3 | C． | 27 | D． | 5 |
分析 求出双曲线的a，b，c，设|PF1|=15，运用双曲线的定义，求得|PF2|=3或27，讨论P在左支和右支上，求出最小值，即可判断P的位置，进而得到所求距离．
解答 解：双曲线$\frac{x^2}{36}-\frac{y^2}{64}=1$的a=6，b=8，c=10，
设左右焦点为F1，F2．
则有双曲线的定义，得||PF1|-|PF2||=2a=12，
可设|PF1|=15，则有|PF2|=3或27，
若P在右支上，则有|PF2|≥c-a=4，
若P在左支上，则|PF2|≥c+a=16，
故|PF2|=3舍去；．
故选：C．
点评 本题考查双曲线的方程和定义，考查分类讨论的思想方法，考查运算能力，属于基础题和易错题．
练习册系列答案
相关题目
8．若某几何体的三视图（单位：cm）如图所示，则该几何体的体积等于（ ）
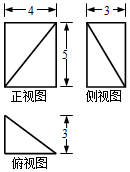
| A． | 10cm3 | B． | 20cm3 | C． | 30cm3 | D． | 40cm3 |
15．如表提供了某厂节能降耗技术改造后在生产A产品过程中纪录的产量x（吨）与相应的生产能耗y（吨）的几组对应数据：
根据上表提供的数据，求得y关于x的线性回归方程为$\widehat{y}$=0.7x+0.35，那么表中n的值为（ ）注（$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$，$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$）
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | n | 4 | 4.5 |
| A． | 3 | B． | 3.15 | C． | 3.5 | D． | 4.5 |
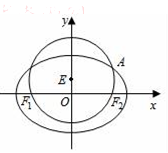已知圆E：x2+（y-$\frac{1}{2}$）2=$\frac{9}{4}$，经过椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左右焦点F1，F2，且与椭圆C在第一象限的交点为A，且F1，E，A三点共线，直线l交椭圆C于M，N两点，且与直线OA平行．
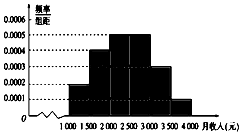某市统计局就某地居民的月收入调查了10000人，并根据所得数据画出样本的频率分布直方图，每个分组包括左端点，不包括右端点，如第一组表示收入在[1000，1500）．
10．已知函数f（x）=sin（2x+ϕ）（其中ϕ是实数），若$f（x）≤|{f（{\frac{π}{6}}）}|$对x∈R恒成立，且$f（{\frac{π}{2}}）＞f（0）$，则f（x）的单调递增区间是（ ）
| A． | [kπ-$\frac{π}{3}$，kπ+$\frac{π}{6}$]（k∈Z） | B． | $[{kπ，kπ+\frac{π}{2}}]（{k∈Z}）$ | C． | $[{kπ+\frac{π}{6}，kπ+\frac{2π}{3}}]（{k∈Z}）$ | D． | $[{kπ-\frac{π}{2}，kπ}]（{k∈Z}）$ |