题目内容
在某海岛A上有一座海拔1千米的山，山顶设有一个观察站P，上午11时，测得一轮船在岛北30°东，俯角为30°的B处，到11时10分又测得该船在岛北60°西、俯角为60°的C处，则船的航行速度是每小时分析：在Rt△PAB和Rt△PAC中分别求得AC和AB，进而在△ACB中利用勾股定理求得BC，进而用里程除以时间求得船的航行速度．
解答：
解：在Rt△PAB中，∠APB=60° PA=1，∴AB=
（千米）
在Rt△PAC中，∠APC=30°，∴AC=
（千米）
在△ACB中，∠CAB=30°+60°=90°
则BC=
=
=
（千米）
÷
=2
（千米/时）
故答案为2
．
解：在Rt△PAB中，∠APB=60° PA=1，∴AB=| 3 |
在Rt△PAC中，∠APC=30°，∴AC=
| ||
| 3 |
在△ACB中，∠CAB=30°+60°=90°
则BC=
| AB2+AC2 |
(
|
| ||
| 3 |
| ||
| 3 |
| 1 |
| 6 |
| 30 |
故答案为2
| 30 |
点评：本题主要考查了解三角形的实际应用，关键在于画出图形，使问题易于理解和掌握．
练习册系列答案
相关题目
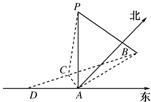如图，在海岛A上有一座海拔1千米的山，山顶设有一个观察站P，上午11时，测得一轮船在岛北偏东30°，俯角为30°的B处，到11时10分又测得该船在岛北偏西60°，俯角为60°的C处．
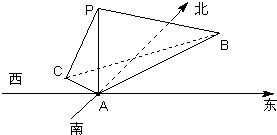在海岛A上有一座海拔1千米的山，山顶设有一个观察站P，上午9时，测得一轮船在岛北偏东30°、俯角为30°的B处，到9时10分又测得该船在岛北西60°、俯角为45°的C处．