题目内容
已知正方形ABCD与正方形ABEF相交,且∠DAF=90°,AB=(1)求证:MN∥平面BCE;
(2)设MN=y,AM=x,求y=f(x)的表达式,并求y的最小值.
(1)证明:过M作MP∥AB交BC于P,
过N作NQ∥AB交BE于Q,连结PQ,∴MP∥QN.
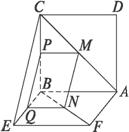
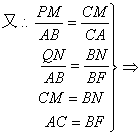 PM=QN
PM=QN
∴MNQP为平行四边形.
 MN∥面BCE.
MN∥面BCE.
(2)解:由(1)可知MN![]() PQ,又由已知AM=FN=x,
PQ,又由已知AM=FN=x,
AB=CB=BE=![]()
![]() AC=BF=2.
AC=BF=2.
在△CBA中,有![]() ,
,
∴![]() (2-x)=BQ.
(2-x)=BQ.
∴MN=PQ=![]() ,
,
即y=![]() .
.
当x=1时,ymin=1.∴M为AC中点时,y取最小值1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
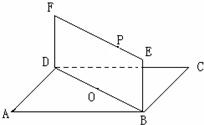 如图,已知正方形ABCD与矩形BEFD所在的平面互相垂直,AB=
如图,已知正方形ABCD与矩形BEFD所在的平面互相垂直,AB=
 ,DF=1,P是线段EF上的动点.
,DF=1,P是线段EF上的动点.
 ,DF=1,P是线段EF上的动点.
,DF=1,P是线段EF上的动点.