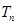题目内容
(本小题14分)
已知![]() ,
,
(1)若![]() ,函数
,函数![]() 在其定义域内是增函数,求
在其定义域内是增函数,求![]() 的取值范围.
的取值范围.
(2)在(1)的结论下,设![]() ,求函数
,求函数![]() 的最小值;
的最小值;
(3)设各项为正的数列![]() 满足:
满足:![]() ,求证:
,求证:![]()
解:(1)依题意:![]() ∵
∵![]() 在
在![]() 递增
递增
∴![]() 对
对![]() 恒成立 ∴
恒成立 ∴![]()
∵![]() ∴
∴![]() 当且仅当
当且仅当![]() 时取“
时取“![]() ”,∴
”,∴![]() ,
,
且当![]() 时,
时,![]() ,
,![]() ,
,![]()
∴符合![]() 在
在![]() 是增函数∴
是增函数∴![]()
(2)设![]() ,∵
,∵![]() ∴
∴![]() , 则函数
, 则函数![]() 化为:
化为:
![]() ,
,![]()
①当![]() 时,即
时,即![]() 时.
时.![]() 在
在![]() 递增 ∴当
递增 ∴当![]() 时,
时,![]()
②当![]() 时,即
时,即![]() ,当
,当![]()
③当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 递减,当
递减,当![]() 时,
时,![]()
综上: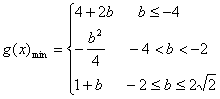
(3)∵![]() ,
,![]()
假设![]() ,则
,则![]() , ∴
, ∴![]() 成立
成立
设![]() ,
,![]() ,则
,则![]()
∴![]() 在
在![]() 单调递减,∴
单调递减,∴![]() ,∴
,∴![]()
∴![]() ,故
,故![]() ,∴
,∴![]()
![]() , ∴
, ∴![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (本小题14分)右图是一个直三棱柱(以
(本小题14分)右图是一个直三棱柱(以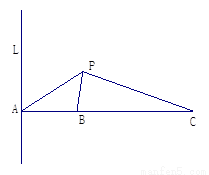
 km,用
km,用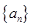 中,
中,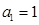 ,前
,前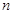 项和
项和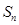 满足条件
满足条件 ,
,
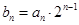 ,求数列
,求数列 的前
的前