题目内容

若对于任意的x>0,不等式≤a恒成立,则实数a的取值范围为　　　　　.

【解析】=≤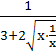=,当且仅当x=1时取等号,所以要使≤a恒成立,则a≥,即实数a的取值范围为a≥.

答案:a≥

【变式备选】已知x>0,y>0,x+2y+2xy=8,则x+2y的最小值是　　　　.

【解析】因为x+2y+2xy=8,所以y=>0,

所以-1<x<8,

所以x+2y=x+2·=(x+1)+-2≥

2-2=4,当且仅当x=2时取等号.

答案:4

练习册系列答案
相关题目

已知函数f(x)＝ex＋ax，g(x)＝exlnx.(e≈2.718 28…)．

(1)设曲线y＝f(x)在x＝1处的切线与直线x＋(e－1)y＝1垂直，求a的值；

(2)若对于任意实数x≥0，f(x)>0恒成立，试确定实数a的取值范围；

(3)当a＝－1时，是否存在实数x0∈[1，e]，使曲线C：y＝g(x)－f(x)在点x＝x0处的切线与y轴垂直？若存在，求出x0的值；若不存在，请说明理由．

已知函数f（x）=lnx－ax（a>0）．

（I）当a=2时，求f（x）的单调区间与极值；

（Ⅱ）若对于任意的x∈（0，+），都有f（x）<0，求a的取值范围．

 

已知函数f(x)＝3x2＋bx＋c，不等式f(x)>0的解集为(－∞，－2)∪(0，＋∞)．　

(1) 求函数f(x)的解析式；

(2) 已知函数g(x)＝f(x)＋mx－2在(2，＋∞)上单调增，求实数m的取值范围；

(3) 若对于任意的x∈[－2,2]，f(x)＋n≤3都成立，求实数n的最大值．

 

已知函数,其中e为自然对数的底数，a

   （I）设a=-1 ,x[-1,1]，求函数y=f(x)的极值；

   （Ⅱ）若对于任意的a>0，都有f(x)成立，求x的取值范围。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网