题目内容
函数f(x)=x+| 2 | x+1 |
分析:先利用配凑法将函数式配成积为定值,再利用基本不等式进行放缩,即可求得函数f(x)=x+
(x>0)的最小值.
| 2 |
| x+1 |
解答:解:∵f(x)=x+
=x+1+
-1≥2
-1,
∴函数f(x)=x+
(x>0)的最小值为:2
-1.
故答案为:2
-1.
| 2 |
| x+1 |
=x+1+
| 2 |
| x+1 |
| 2 |
∴函数f(x)=x+
| 2 |
| x+1 |
| 2 |
故答案为:2
| 2 |
点评:本小题主要考查函数的最值及其几何意义、基本不等式、不等式的解法等基础知识,考查运算求解能力、化归与转化思想.属于基础题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
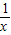 是奇函数”的证明不是综合法的是( )
是奇函数”的证明不是综合法的是( )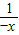 =-(x+
=-(x+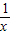 )=-f(x),∴f(x)是奇函数
)=-f(x),∴f(x)是奇函数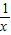 +(-x)+(-
+(-x)+(-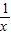 )=0,∴f(x)=-f(-x),∴f(x)是奇函数
)=0,∴f(x)=-f(-x),∴f(x)是奇函数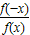 =
=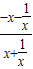 =-1,∴f(-x)=-f(x),∴f(x)是奇函数
=-1,∴f(-x)=-f(x),∴f(x)是奇函数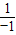 =-2,又f(1)=1+
=-2,又f(1)=1+ =2
=2