Question

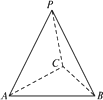
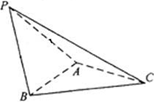
如下图,在三棱锥P—ABC中,AB⊥BC,AB=BC,点O,D分别是AC,PC的中点,OP⊥平面ABC.

求证:直线OD∥平面PAB.

Answer 1

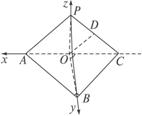
证明：因为AB=BC,O为AC的中点,

所以OB⊥AC,OA=OB=OC.如右图建立空间直角坐标系,

设OA=a,则A(a,0,0),B(0,a,0),C(-a,0,0),P(0,0,b),则D(-,0,).

所以=(-,0,).

设平面PAB的法向量为n=(x,y,z),

则

由于=（a,0,-b）,=(-a,a,0).

所以

令z=,则x=y=1,

所以n=(1,1,).所以·n==0.

所以⊥n.

又因为OD不在平面PAB内.

所以OD∥平面PAB.