题目内容
已知向量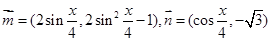 ,函数
,函数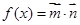 .
.
(1) 求函数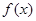 的最大值,并写出相应
的最大值,并写出相应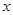 的取值集合;
的取值集合;
(2) 若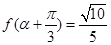 ,且
,且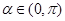 ,求
,求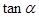 的值.
的值.
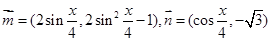 ,函数
,函数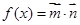 .
.(1) 求函数
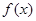 的最大值,并写出相应
的最大值,并写出相应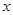 的取值集合;
的取值集合;(2) 若
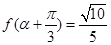 ,且
,且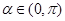 ,求
,求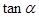 的值.
的值.(1)当 时,
时, 。
。
(2) 。
。
 时,
时, 。
。(2)
 。
。试题分析:

所以,当
 ,即当
,即当 时,
时, 。
。(2)由(1)得:
 ,所以
,所以 ,从而
,从而 。
。由于
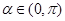 ,所以
,所以 。
。于是,
 。
。点评:中档题,在研究三角函数的性质过程中,往往要利用三角函数公式进行“化一”,即完成三角函数恒等变换。应用同角公式的平方关系时,应注意开方“+、-”d的选用。

练习册系列答案
相关题目
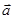 =(cos
=(cos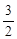 x,sin
x,sin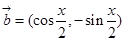 ,且x∈[0,
,且x∈[0,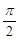 ].
].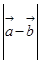
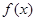 =
=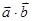 ,求函数
,求函数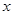 的值。
的值。 ,向量
,向量 向量
向量 ,且
,且 的最小正周期为
的最小正周期为 .
. 的解析式;
的解析式; 、
、 、
、 分别为
分别为 内角
内角 所对的边,且
所对的边,且 ,
,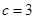 ,又
,又 恰
恰 上的最小值,求
上的最小值,求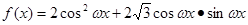 ,(其中
,(其中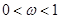 ),若直线
),若直线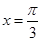 是函数
是函数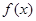 图象的一条对称轴。
图象的一条对称轴。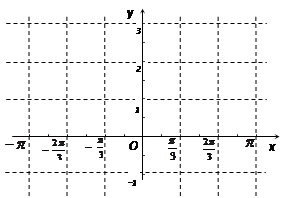
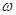 的值;
的值;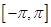 上的图象.
上的图象.
 的最小正周期及单调递增区间;
的最小正周期及单调递增区间; 中,若
中,若 ,
, ,
, ,求
,求 的值.
的值. 在区间
在区间 的简图是( )
的简图是( )
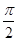 ,π]的最大值是________.
,π]的最大值是________. 中,已知内角
中,已知内角 ,边
,边 .设内角
.设内角 ,
, .
. 的解析式和定义域;
的解析式和定义域;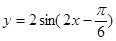 .
.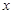 的取值集合,并写出最大值。
的取值集合,并写出最大值。