题目内容
设![]() 曲线
曲线![]() 有4个不同的交点.
有4个不同的交点.
(Ⅰ)求θ的取值范围;
(Ⅱ)证明这4个交点共圆,并求圆半径的取值范围.
(Ⅰ)![]() 的取值范围为(0,
的取值范围为(0,![]() (Ⅱ)r的取值范围是
(Ⅱ)r的取值范围是![]()
解析:
(I)两曲线的交点坐标(x,y)满足方程组
![]() 即
即![]()
有4个不同交点等价于![]() 且
且![]() 即
即![]()
又因为![]() 所以得
所以得![]() 的取值范围为(0,
的取值范围为(0,![]()
(II)由(I)的推理知4个交点的坐标(x,y)满足方程
![]()
即得4个交点共圆,该圆的圆心在原点,半径为![]()
因为![]() 在
在![]() 上是减函数,所以由
上是减函数,所以由![]()
知r的取值范围是![]()

练习册系列答案
相关题目
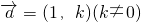 的直线l,使得l与曲线C交与两个不同的点M,N,且有
的直线l,使得l与曲线C交与两个不同的点M,N,且有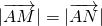 ?若存在,求出k的取值范围;若不存在,说明理由.
?若存在,求出k的取值范围;若不存在,说明理由. 的直线l,使得l与曲线C交与两个不同的点M,N,且有
的直线l,使得l与曲线C交与两个不同的点M,N,且有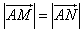 ?若存在,求出k的取值范围;若不存在,说明理由。
?若存在,求出k的取值范围;若不存在,说明理由。  的直线l,使得l与曲线C交与两个不同的点M,N,且有
的直线l,使得l与曲线C交与两个不同的点M,N,且有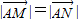 ?若存在,求出k的取值范围;若不存在,说明理由.
?若存在,求出k的取值范围;若不存在,说明理由.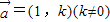 的直线l,使得l与曲线C交与两个不同的点M,N,且有
的直线l,使得l与曲线C交与两个不同的点M,N,且有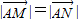 ?若存在,求出k的取值范围;若不存在,说明理由.
?若存在,求出k的取值范围;若不存在,说明理由.