题目内容
已知函数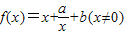 .,其中a,b∈R
.,其中a,b∈R(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)若对于任意的
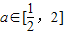 ,不等式f(x)≤10在
,不等式f(x)≤10在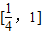 上恒成立,求b的取值范围.
上恒成立,求b的取值范围.
【答案】分析:(I)先确定函数的定义域然后求导数fˊ(x),在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0;讨论函数f(x)的单调性即可;
(Ⅱ)由(Ⅰ)知,f(x)在[ ,1]上的最大值为
,1]上的最大值为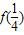 与f(1)中的较大者,对于任意的a∈[
与f(1)中的较大者,对于任意的a∈[ ,2],不等式f(x)≤10在[
,2],不等式f(x)≤10在[ ,1]上恒成立,利用函数的最值列出关于a,b的不等关系,从而得满足条件的b的取值范围.
,1]上恒成立,利用函数的最值列出关于a,b的不等关系,从而得满足条件的b的取值范围.
解答:解:(Ⅰ)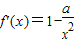 ,
,
当a≤0时,显然f'(x)>0(x≠0),这时f(x)在(-∞,0),(0,+∞)内是增函数;
当a>0时,令f'(x)=0,解得x=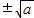 ,
,
当x变化时,f'(x),f(x)的变化情况如下表:
所以f(x)在(-∞,-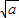 ),(
),(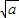 ,+∞)内是增函数,在(-
,+∞)内是增函数,在(-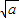 ,0),(0,
,0),(0,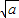 )内是减函数
)内是减函数
(Ⅱ)由(Ⅰ)知,f(x)在[ ,1]上的最大值为
,1]上的最大值为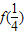 与f(1)中的较大者,对于任意的a∈[
与f(1)中的较大者,对于任意的a∈[ ,2],不等式f(x)≤10在[
,2],不等式f(x)≤10在[ ,1]上恒成立,当且仅当
,1]上恒成立,当且仅当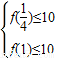 ,即
,即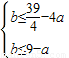 ,对任意的a∈[
,对任意的a∈[ ,2]成立.从而得b≤
,2]成立.从而得b≤ ,所以满足条件的b的取值范围是(-∞,
,所以满足条件的b的取值范围是(-∞, ].
].
点评:本题考查了函数的单调性,利用导数判断函数的单调性的步骤是:(1)确定函数的定义域;(2)求导数fˊ(x);(3)在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0;(4)确定函数的单调区间.若在函数式中含字母系数,往往要分类讨论.
(Ⅱ)由(Ⅰ)知,f(x)在[
 ,1]上的最大值为
,1]上的最大值为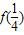 与f(1)中的较大者,对于任意的a∈[
与f(1)中的较大者,对于任意的a∈[ ,2],不等式f(x)≤10在[
,2],不等式f(x)≤10在[ ,1]上恒成立,利用函数的最值列出关于a,b的不等关系,从而得满足条件的b的取值范围.
,1]上恒成立,利用函数的最值列出关于a,b的不等关系,从而得满足条件的b的取值范围.解答:解:(Ⅰ)
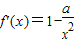 ,
,当a≤0时,显然f'(x)>0(x≠0),这时f(x)在(-∞,0),(0,+∞)内是增函数;
当a>0时,令f'(x)=0,解得x=
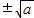 ,
,当x变化时,f'(x),f(x)的变化情况如下表:
| x | (-∞,-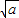 ) ) | -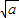 | (-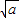 ,0) ,0) | (0,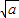 ) ) | 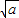 | (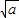 ,+∞) ,+∞) |
| f'(x) | + | - | - | + | ||
| f(x) | ↗ | 极大值 | ↘ | ↘ | 极小值 | ↗ |
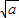 ),(
),(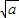 ,+∞)内是增函数,在(-
,+∞)内是增函数,在(-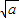 ,0),(0,
,0),(0,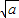 )内是减函数
)内是减函数(Ⅱ)由(Ⅰ)知,f(x)在[
 ,1]上的最大值为
,1]上的最大值为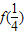 与f(1)中的较大者,对于任意的a∈[
与f(1)中的较大者,对于任意的a∈[ ,2],不等式f(x)≤10在[
,2],不等式f(x)≤10在[ ,1]上恒成立,当且仅当
,1]上恒成立,当且仅当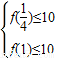 ,即
,即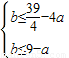 ,对任意的a∈[
,对任意的a∈[ ,2]成立.从而得b≤
,2]成立.从而得b≤ ,所以满足条件的b的取值范围是(-∞,
,所以满足条件的b的取值范围是(-∞, ].
].点评:本题考查了函数的单调性,利用导数判断函数的单调性的步骤是:(1)确定函数的定义域;(2)求导数fˊ(x);(3)在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0;(4)确定函数的单调区间.若在函数式中含字母系数,往往要分类讨论.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案
相关题目
 .,其中a,b∈R
.,其中a,b∈R ,
, (其中A>0,
(其中A>0, >0,
>0, <
<
 的部分图象如图所示,求这个函数的解析式.
的部分图象如图所示,求这个函数的解析式.
 满足
满足 ,其中a>0,a≠1.
,其中a>0,a≠1.
 的值为负数,求
的值为负数,求 的取值范围。
的取值范围。 (其中A>0,
(其中A>0, )的图象如图所示。
)的图象如图所示。
 的值。
的值。