Question

（2013•乐山二模）已知定义在R上的函数y=f（x）满足f（x+2）=f（x），当-1＜x≤1时，f（x）=x³．若函数g（x）=f（x）-log_a|x|恰有6个零点，则a（　　）

• A．a=5或a=

  1

  5

• B．a∈(0，

  1

  5

  )∪[5，+∞)
• C．a∈[

  1

  7

  ，

  1

  5

  ]∪[5，7]
• D．a∈[

  1

  7

  ，

  1

  5

  )∪[5，7)

Answer 1

分析：本题通过典型的作图画出log_a|x|以及f（x）的图象，从图象交点上交点的不同，来判断函数零点个数，从而确定底数a的大小范围

解答：解：首先将函数g（x）=f（x）-log_a|x|恰有6个零点，这个问题转化成f（x）=log_a|x|的交点来解决．
数形结合：如图，f（x+2）=f（x），知道周期为2，当-1＜x≤1时，f（x）=x³图象可以画出来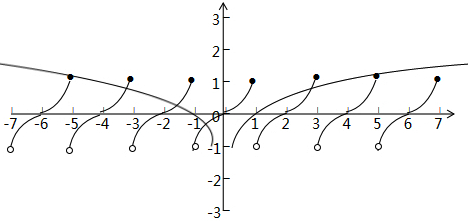，同理左右平移各2个单位，得到在（-7，7）上面的图象，以下分两种情况：
（1）当a＞1时，log_a|x|如图所示，左侧有4个交点，右侧2个，
此时应满足log_a5≤1＜log_a7，即log_a5≤log_aa＜log_a7，所以5≤a＜7．
（2）当0＜a＜1时，log_a|x|与f（x）交点，左侧有2个交点，右侧4个，
此时应满足log_a5＞-1，log_a7≤-1，即log_a5＜-log_aa≤log_a7，所以5＜a^-1≤7．故

1

7

≤a＜

1

5

综上所述，a的取值范围是：5≤a＜7或

1

7

≤a＜

1

5

故选D选项

点评：本题考查函数零点应用转化为两个函数交点来判断，又综合了奇函数对称性对数运算等知识，属于较难的一类题，端点也要认真考虑，极容易漏掉端点