题目内容
已知AB是椭圆
+
=1上不垂直于对称轴的弦,M为AB中点,O为坐标原点,设直线AB和直线OM斜率分别为k1,k2,则k1•k2=
| x2 |
| 4 |
| y2 |
| 3 |
-
| 3 |
| 4 |
-
.| 3 |
| 4 |
分析:利用“点差法”、中点坐标公式、斜率计算公式即可得出.
解答:解:设A(x1,y1),B(x2,y2),M(x0,y0),则
,k1=
,k2=
.
∵
+
=1,
+
=1,
∴
+
=0.
∴
+
k1=0,∴
+
=0.
∴k1k2=-
.
故答案为-
.
|
| y1-y2 |
| x1-x2 |
| y0 |
| x0 |
∵
| ||
| 4 |
| ||
| 3 |
| ||
| 4 |
| ||
| 3 |
∴
| (x1+x2)(x1-x2) |
| 4 |
| (y1+y2)(y1-y2) |
| 3 |
∴
| 2x0 |
| 4 |
| 2y0 |
| 3 |
| 1 |
| 4 |
| k1k2 |
| 3 |
∴k1k2=-
| 3 |
| 4 |
故答案为-
| 3 |
| 4 |
点评:本题考查了椭圆的标准方程、“点差法”、中点坐标公式、斜率计算公式等基础知识与基本技能方法,属于中档题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
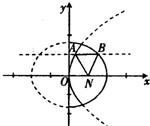 已知定点N(1,0),动点A、B分别在图中抛物线y2=4x及椭圆
已知定点N(1,0),动点A、B分别在图中抛物线y2=4x及椭圆