题目内容
选修4—5:不等式选讲
已知 ,证明:
,证明: .
.
详见解析
【解析】
试题分析:由基本不等式得 ,
, ,再根据不等式性质得:
,再根据不等式性质得:
试题解析:因为
所以 , 4分
, 4分
 , 8分
, 8分
所以 . 10分
. 10分
考点:基本不等式证不等式
考点分析: 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案
相关题目
(本小题满分16分)已知数列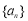 (
( ,
,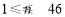 )满足
)满足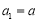 ,
,  其中
其中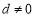 ,
,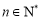 .
.
(1)当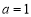 时,求
时,求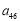 关于
关于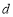 的表达式,并求
的表达式,并求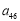 的取值范围;
的取值范围;
(2)设集合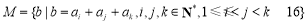 .
.
①若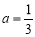 ,
,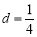 ,求证:
,求证: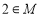 ;
;
②是否存在实数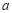 ,
,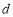 ,使
,使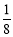 ,
,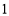 ,
,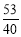 都属于
都属于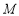 ?若存在,请求出实数
?若存在,请求出实数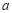 ,
,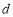 ;若不存在,请说明理由.
;若不存在,请说明理由.
(本小题12分)据报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改革”引起广泛关注,为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人进行调查,就“是否取消英语听力”问题进行了问卷调查统计,结果如下表:
态度 调查人群 | 应该取消 | 应该保留 | 无所谓 |
在校学生 | 2100人 | 120人 |
|
社会人士 | 600人 |
|
|
已知在全体样本中随机抽取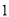 人,抽到持“应该保留”态度的人的概率为
人,抽到持“应该保留”态度的人的概率为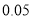
(1)现用分层抽样的方法在所有参与调查的人中抽取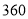 人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)已知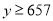 ,
, ,若所选择的在校学生的人数低于被调查人群总数的80%,则认为本次调查“失效”,求本次调查“失效”的概率.
,若所选择的在校学生的人数低于被调查人群总数的80%,则认为本次调查“失效”,求本次调查“失效”的概率.
 的最小正周期为 .
的最小正周期为 . 的焦点为顶点,顶点为中心,离心率为2的双曲线标准方程为 .
的焦点为顶点,顶点为中心,离心率为2的双曲线标准方程为 .
 ,则函数
,则函数 的值域为 .
的值域为 . 的离心率为
的离心率为 ,则实数a的值为 .
,则实数a的值为 .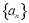 的公比为
的公比为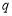 (
(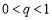 ),前n项和为
),前n项和为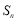 ,若
,若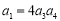 ,且
,且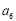 与
与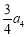 的等差中项为
的等差中项为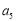 ,则
,则 .
. 人
人 人
人 人
人 中,
中,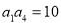 ,则数列
,则数列 的前
的前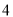 项和等于( )
项和等于( )