题目内容
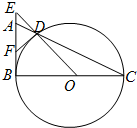 如图,在△ABC中,∠ABC=90°,以BC为直径的圆O交AC于点D,连接OD,并延长交BA的延长线于点E,圆O的切线DF交EB于F
如图,在△ABC中,∠ABC=90°,以BC为直径的圆O交AC于点D,连接OD,并延长交BA的延长线于点E,圆O的切线DF交EB于F
(Ⅰ)证明:AF=BF;
(Ⅱ)若ED=8,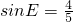 ,求OC的长.
,求OC的长.
(Ⅰ)证明:∵BC为圆O的直径,DF为圆O的切线
∴DF=BF,DF⊥OD
∴∠ODC+∠ADF=90°
∵∠ABC=90°,∴∠C+∠BAC=90°
∵OD=OC,∴∠ODC=∠C
∴∠ADF=∠BAC
∴AF=DF
∵DF=BF,∴AF=BF;
(Ⅱ)解:在直角△EBO中,∵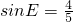 ,
,
∴
∵ED=8,
∴
∴OC=32
分析:(Ⅰ)利用BC为圆O的直径,DF为圆O的切线,可得DF=BF,DF⊥OD,再证明∠ADF=∠BAC,从而AF=DF,故可证AF=BF;
(Ⅱ)在直角△EBO中,利用 ,即可求得OC的长.
,即可求得OC的长.
点评:本题是选考题,考查圆的性质,解题的关键是利用圆的切线性质,属于基础题.
∴DF=BF,DF⊥OD
∴∠ODC+∠ADF=90°
∵∠ABC=90°,∴∠C+∠BAC=90°
∵OD=OC,∴∠ODC=∠C
∴∠ADF=∠BAC
∴AF=DF
∵DF=BF,∴AF=BF;
(Ⅱ)解:在直角△EBO中,∵
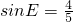 ,
,∴

∵ED=8,
∴

∴OC=32
分析:(Ⅰ)利用BC为圆O的直径,DF为圆O的切线,可得DF=BF,DF⊥OD,再证明∠ADF=∠BAC,从而AF=DF,故可证AF=BF;
(Ⅱ)在直角△EBO中,利用
 ,即可求得OC的长.
,即可求得OC的长.点评:本题是选考题,考查圆的性质,解题的关键是利用圆的切线性质,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=
如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,
如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm, 如图,在△ABC中,设
如图,在△ABC中,设 如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3.
如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3. 如图,在△ABC中,已知
如图,在△ABC中,已知