题目内容
在极坐标系中,圆C的方程为ρ=2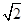 sin
sin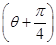 ,以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,直线
,以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,直线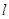 的参数方程为
的参数方程为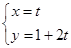 (t为参数),判断直线
(t为参数),判断直线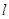 和圆C的位置关系.
和圆C的位置关系.
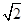 sin
sin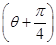 ,以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,直线
,以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,直线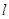 的参数方程为
的参数方程为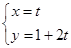 (t为参数),判断直线
(t为参数),判断直线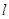 和圆C的位置关系.
和圆C的位置关系.直线l和⊙C相交.
试题分析:先利用三角函数正弦的和角公式将圆C的极坐标方程化为:ρ=2(sinθ+cosθ),再将两边同时乘以ρ得到ρ2=2(ρsinθ+ρcosθ),又因为是以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,所以只须将
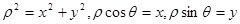 代入即得圆C的直角坐标方程,化成标准形式,可写出圆C的圆心坐标和半径,再将直线
代入即得圆C的直角坐标方程,化成标准形式,可写出圆C的圆心坐标和半径,再将直线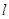 的参数方程为
的参数方程为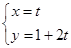 ,(t为参数)消去参数t,到直线
,(t为参数)消去参数t,到直线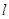 的普通方程,再由点到直线的距离公式
的普通方程,再由点到直线的距离公式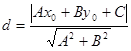 算出圆C的圆心到直线
算出圆C的圆心到直线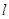 的距离,与圆C的半径比较大小:当d>r时,直线与圆相离,当d=时,直线与圆相切,当d<r时,直线与圆相交;得出结论.
的距离,与圆C的半径比较大小:当d>r时,直线与圆相离,当d=时,直线与圆相切,当d<r时,直线与圆相交;得出结论.试题解析:消去参数t,得直线l的直角坐标方程为y=2x+1;
ρ=2
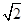 sin
sin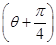 即ρ=2(sinθ+cosθ),
即ρ=2(sinθ+cosθ),两边同乘以ρ得ρ2=2(ρsinθ+ρcosθ),
得圆C的直角坐标方程为(x-1)2+(y-1)2=2,
圆心C到直线l的距离d=
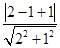 =
=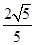 <
<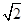 ,
,所以直线l和⊙C相交.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
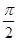 ).若直线l过点P,且倾斜角为
).若直线l过点P,且倾斜角为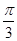 ,圆C以M为圆心, 4为半径.
,圆C以M为圆心, 4为半径.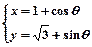 ,(θ为参数).表示的曲线为C,
,(θ为参数).表示的曲线为C, 到曲线
到曲线 上的点的距离的最小值为 .
上的点的距离的最小值为 .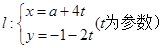 ,圆
,圆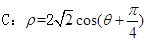 (极轴与x轴非负半轴重合,且单位长度相同),若直线l被圆C截得的弦长为
(极轴与x轴非负半轴重合,且单位长度相同),若直线l被圆C截得的弦长为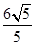 ,则实数a的值为 .
,则实数a的值为 .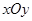 中,直线
中,直线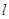 的参数方程为
的参数方程为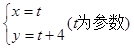 .曲线
.曲线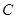 的参数方程为
的参数方程为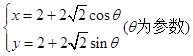 ,则直线
,则直线 个
个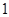 个
个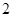 个
个 的直线
的直线 与曲线
与曲线 有公共点,则直线
有公共点,则直线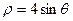 化为直角坐标方程为 .
化为直角坐标方程为 .