题目内容
如图，已知四面体AJ3GD的各棱长都相等，E为棱BC的中点，则二面角E-AD-C的余弦值为
分析：取AD的中点F，连接EF，CF，易证EF⊥AD，而CF⊥AD，则∠EFC为二面角E-AD-C的平面角，在三角形EFC中求出此角的余弦值即可．
解答：解：
取AD的中点F，连接EF，CF
设正四面体的边长为2，则AE=
，ED=
，EF=
∵AE=ED∴EF⊥AD，而CF⊥AD
∴∠EFC为二面角E-AD-C的平面角
而CF=
，EC=1
∴cos∠EFC=
=
=
故答案为：
取AD的中点F，连接EF，CF设正四面体的边长为2，则AE=
| 3 |
| 3 |
| 2 |
∵AE=ED∴EF⊥AD，而CF⊥AD
∴∠EFC为二面角E-AD-C的平面角
而CF=
| 3 |
∴cos∠EFC=
| EF |
| CF |
| ||
|
| ||
| 3 |
故答案为：
| ||
| 3 |
点评：本题主要考查了正四面体的性质，以及二面角的平面角及求法，解决此类问题的关键是寻找二面角的平面角，同时考查空间想象能力，属于基础题．
练习册系列答案
相关题目
如图，已知四面体P-ABC中，PA=PB=PC，且AB=AC，∠BAC=90°，则异面直线PA与BC所成的角为
如图，已知四面体ABCD的四个面均为锐角三角形，EFGH分别是边AB，BC，CD，DA上的点，BD||平面EFGH，且EH=FG．
（2011•焦作一模）如图：已知四面体PABC的所有棱长均为3cm，E、F分别是棱PC，PA上的点，且
如图，已知四面体A-BCD的四个顶点都在球M的球面上，BD=2，其余棱长均为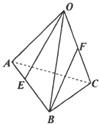
如图，已知四面体O-ABC中，E、F分别为AB，OC上的点，且AE=