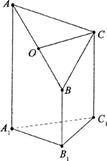
题目内容
设点O是△ABC的三边中垂线的交点，且AC2-2AC+AB2=0，则
•
的范围是
| BC |
| AO |
[-
，2）
| 1 |
| 4 |
[-
，2）
．| 1 |
| 4 |
分析：先利用余弦定理，确定AB，AC，利用向量的数量积，化简
•
，再利用配方法确定其范围，即可得到结论．
| BC |
| AO |
解答：解：设圆的半径为R，∠AOB为α，∠AOC为β，则
AB2=AO2+BO2-2AO×BOcosα=2R2-2R2 cosα，AC2=AO2+CO2-2AO×COcosβ=2R2-2R2cosβ
∴
•
=
•(
+
)=
•
+
•
=R2 cosα-R2cosβ=
∵AC2-2AC+AB2=0，∴
=AC2-AC=(AC-
)2-
∵AC2-2AC=-AB2＜0，0＜AC＜2
∴-
≤
＜2
∴
•
的范围是[-
，2）
故答案为：[-
，2）．
AB2=AO2+BO2-2AO×BOcosα=2R2-2R2 cosα，AC2=AO2+CO2-2AO×COcosβ=2R2-2R2cosβ
∴
| AO |
| BC |
| AO |
| BO |
| OC |
| AO |
| BO |
| AO |
| OC |
| AC2-AB2 |
| 2 |
∵AC2-2AC+AB2=0，∴
| AC2-AB2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
∵AC2-2AC=-AB2＜0，0＜AC＜2
∴-
| 1 |
| 4 |
| AC2-AB2 |
| 2 |
∴
| BC |
| AO |
| 1 |
| 4 |
故答案为：[-
| 1 |
| 4 |
点评：本题考查数量积运算，考查三角形的外心，考查配方法求函数的值域，有一定的综合性．
练习册系列答案
相关题目
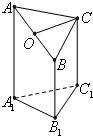如图是一个直三棱柱（以A1B1C1为底面）被一平面所截得到的几何体，截面为ABC．已知A1B1=B1C1=1，∠A1B1C1=90°，AA1=4，BB1=2，CC1=3．
如图是一个直三棱柱（以A1B1C1为底面）被一平面所截得到的几何体，截面为ABC已知A1B1=B1C1=1，∠A1B1C1=90°，AA1=4，BB1=2，CC1=3
如图是一个直三棱柱（以A1B1C1为底面）被一平面所截得到的几何体，截面为ABC．已知A1B1=B1C1=2，∠A1B1C1=90°，AA1=4，BB1=2，CC1=3．
右图是一个直三棱柱（以A1B1C1为底面），被一平面所截得的几何体，截面为ABC．已知A1B1=B1C1=1，∠A1B1C1=900，AA1=4，BB1=2，CC1=3