题目内容
设p：
．使得p是q的必要但不充分条件的实数a的取值范围是
- A.（-∞，0）
- B.（-∞-2]
- C.[-2，3]
- D.[3，+∞）
A
分析：先化简命题p，通过解分式不等式化简命题q，将p是q的必要不充分条件转化为{x|x＞1或x＜
}是{x|
}的子集，根据集合的包含关系，列出不等式组求出a的范围．
解答：∵p：|2x+1|＞a，
∴2x+1＞a或2x+1＜-a，
；
q：
，
∴x＞1或x＜；
∵p是q的必要不充分条件
∴有{x|x＞1或x＜}是{x|}的子集
∴
解得a＜1且a＜0
∴a＜0．
故选A．
点评：判断一个命题是另一个命题的什么条件问题，应该先化简各个命题，然后再进行判断，若命题中是数集，常转化为集合的包含关系来解决，本题是一个易错题．
分析：先化简命题p，通过解分式不等式化简命题q，将p是q的必要不充分条件转化为{x|x＞1或x＜
}是{x|}的子集，根据集合的包含关系，列出不等式组求出a的范围．解答：∵p：|2x+1|＞a，
∴2x+1＞a或2x+1＜-a，
；q：
，∴x＞1或x＜
；∵p是q的必要不充分条件
∴有{x|x＞1或x＜
}是{x|}的子集∴
解得a＜1且a＜0
∴a＜0．
故选A．
点评：判断一个命题是另一个命题的什么条件问题，应该先化简各个命题，然后再进行判断，若命题中是数集，常转化为集合的包含关系来解决，本题是一个易错题．
练习册系列答案
高中必刷题系列答案
相关题目
设命题：p：向量
与
共线，命题q：有且只有一个实数λ，使得
=
，则p是q的（ ）
| b |
| a |
| b |
| λa |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
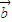与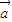
共线，命题q：有且只有一个实数λ，使得
=
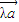，则p是q的（ ）