题目内容
(09年山东实验中学诊断三理)(13分)已知椭圆![]() 的上、下焦点分别为
的上、下焦点分别为![]() ,点
,点![]() 为坐标平面的动点,满足
为坐标平面的动点,满足![]()
![]() (1)求动点
(1)求动点![]() 的轨迹
的轨迹![]() 的方方程;
的方方程;
![]() (2)过点
(2)过点![]() 作曲线
作曲线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,求直线
,求直线![]() 的方程;
的方程;
![]() (3)在直线
(3)在直线![]() 上是否存在点
上是否存在点![]() ,过该点的坐标:若不存在。试说明理由
,过该点的坐标:若不存在。试说明理由
![]()
![]()
![]() 解析:(1)因为
解析:(1)因为![]() 为椭圆
为椭圆![]() 的上、下焦点,所以
的上、下焦点,所以![]() 设
设![]() 。
。
所以 ![]()
因为 ![]()
所以![]() ,整理可得
,整理可得![]()
所以所求动点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]()
![]()
![]() (2)(法一)设过点
(2)(法一)设过点![]() 所作曲线的切线的斜率为
所作曲线的切线的斜率为![]() ,则切线方程为
,则切线方程为![]()
![]()
![]() 由
由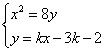 可得:
可得:![]()
![]()
![]()
![]() ,所以
,所以![]() 或
或![]()
![]()
![]() 过点
过点![]() 所作曲线的切线方程为
所作曲线的切线方程为![]() 和
和![]()
![]()
![]() 由
由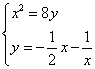 和
和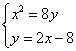 可分别解得:
可分别解得:![]() 和
和![]()
![]()
![]() 所以直线
所以直线![]() 的方程的方程为:
的方程的方程为:![]()
![]()
![]() (法二)设过点
(法二)设过点![]() 所作曲线的两切线的切点为
所作曲线的两切线的切点为![]() ,
,
![]()
![]() 则
则![]() 记
记![]() 则
则![]() ,
,
![]()
![]() 则两条切线的方程为
则两条切线的方程为![]()
![]()
![]() 即
即![]()
![]()
![]() 和
和![]()
![]()
![]() 即:
即:![]()
![]()
![]() 因为两条切线均经过点
因为两条切线均经过点![]() ,所以
,所以![]() 且
且![]()
![]()
![]() 所以 直线
所以 直线![]() 的方程的方程为:
的方程的方程为:![]()
![]()
![]() (3)若
(3)若![]() 存在,不妨设其坐标为
存在,不妨设其坐标为![]() ,过
,过![]() 点所作曲线
点所作曲线![]() 的切线斜率为
的切线斜率为![]() ,
,
![]()
![]() 则切线方程为
则切线方程为![]() ,即
,即![]()
![]()
![]() 由
由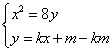 可得:
可得:![]()
![]() 因为直线和抛物线相切,所以
因为直线和抛物线相切,所以![]()
![]() 设两条切线的斜率分别为
设两条切线的斜率分别为![]() ,则
,则![]()
![]() 因为
因为![]() 所以
所以![]()
![]() 所以 两条切线垂直 所以
所以 两条切线垂直 所以![]() 所以
所以![]()
![]() 所以 在直线
所以 在直线![]() 上是存在点
上是存在点![]() 满足题意。
满足题意。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目